В прямокутному трикутнику катет = 12 см,утворює з гіпотенузою кут 30(градусів). Знайти бісектрису другого гострого кута.
Ответы
Ответ дал:
0
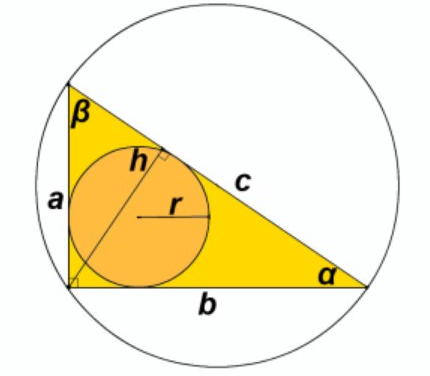
Дано: а= 12см. β=30.
Знайти: (бісектриса кута α)
(бісектриса кута α)
Розв'язання:
α=90-β=90-30=60 градусів.
Синус кута α - це відношення протилежного катета до гіпотенузи
Виразимо гіпотенузу

За т. Піфагора другий катет

Бісектриса другого гострого кута:

Відповідь: 8 см.
Знайти:
Розв'язання:
α=90-β=90-30=60 градусів.
Синус кута α - це відношення протилежного катета до гіпотенузи
Виразимо гіпотенузу
За т. Піфагора другий катет
Бісектриса другого гострого кута:
Відповідь: 8 см.
Приложения:
Ответ дал:
0
б).Бічна сторона рівнобедреного трикутника точкою дотику вписаного кола ділиться у відношенні 9:8, рахуючи від вершини трикутника. Знайдіть площу трикутника якщо радіус вписаного кола дорівнює 16 см
Вас заинтересует
2 года назад
8 лет назад
10 лет назад