1) Острые углы прямоугольного треугольника равны 86 и 4 градусам. Найти угол между медианой и высотой,проведенной из прямого угла.
Ответы
Ответ дал:
0
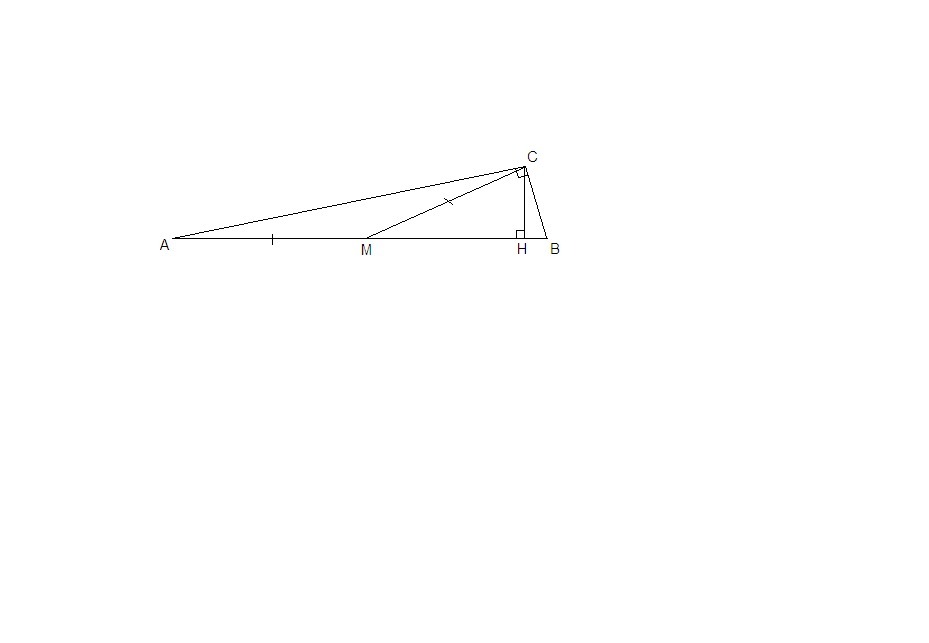
Пусть в треугольнике АВС ∠АСВ = 90°, ∠ВАС = 4°, ∠АВС = 86°.
СМ - медиана, СH - высота.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, значит
СМ = АМ = МВ.
Значит ΔСАМ равнобедренный, ∠МАС = ∠МСА = 4°.
В прямоугольном треугольнике СВН ∠ВСН = 90° - ∠СВН = 90° - 86° = 4°, так как сумма острых углов прямоугольного треугольника равна 90°.
∠МСН = ∠АСВ - ∠МСА - ∠ВСН = 90° - 4° - 4° = 82°
СМ - медиана, СH - высота.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, значит
СМ = АМ = МВ.
Значит ΔСАМ равнобедренный, ∠МАС = ∠МСА = 4°.
В прямоугольном треугольнике СВН ∠ВСН = 90° - ∠СВН = 90° - 86° = 4°, так как сумма острых углов прямоугольного треугольника равна 90°.
∠МСН = ∠АСВ - ∠МСА - ∠ВСН = 90° - 4° - 4° = 82°
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад