Question

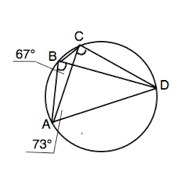
Четырехугольник ABCD вписан в окружность. Угол ABD равен 67°, угол CAD равен 73°. Найдите угол ABC . Ответ дайте в градусах.

Answer 1

Вписанные углы, опирающиеся на одну дугу, равны. Вписанные углы АВD и ACD опираются на дугу АD ⇒ угол АСD=67°.

Сумма углов треугольника 180°. Угол АDC=180°-(67°+73°)=40°

Сумма противоположных углов вписанного четырехугольника равна 180°

Угол АВС+угол АDC=180°⇒ Угол АВС=180°- угол АDC

Угол АВС=180°-40°=140°