диаметр CD окружности с центром в точке O пересекается с хордой AB в точке K, OK-5 см.Расстояние от центра окружности до хорды равно 4 см.Найдите радиус окружности, если длина хорды равна 16 см.
Ответы
Ответ дал:
0
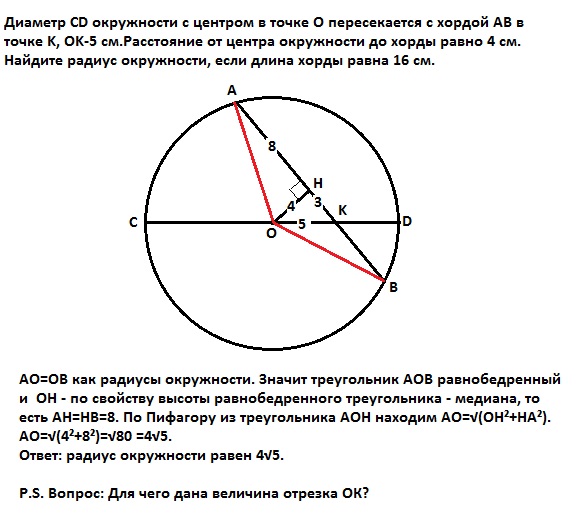
АО=ОВ как радиусы окружности. Значит треугольник АОВ равнобедренный и ОН - по свойству высоты равнобедренного треугольника - медиана, то есть АН=НВ=8см.
По Пифагору из треугольника АОН находим АО=√(ОН²+НА²).
АО=√(4²+8²)=√80 =4√5см.
Ответ: радиус окружности равен 4√5см.
P.S. Вопрос: Для чего дана величина отрезка ОК?
По Пифагору из треугольника АОН находим АО=√(ОН²+НА²).
АО=√(4²+8²)=√80 =4√5см.
Ответ: радиус окружности равен 4√5см.
P.S. Вопрос: Для чего дана величина отрезка ОК?
Приложения:
Вас заинтересует
2 года назад
2 года назад
11 лет назад