Question

Плоскости a и b пересекаются по прямой c. Прямая a лежит в плоскости a. Докажите, что если: а) a пересекает плоскость b в точке A, то A принадлежит прямой c; б) a параллельна плоскости b, то она параллельна прямой c.

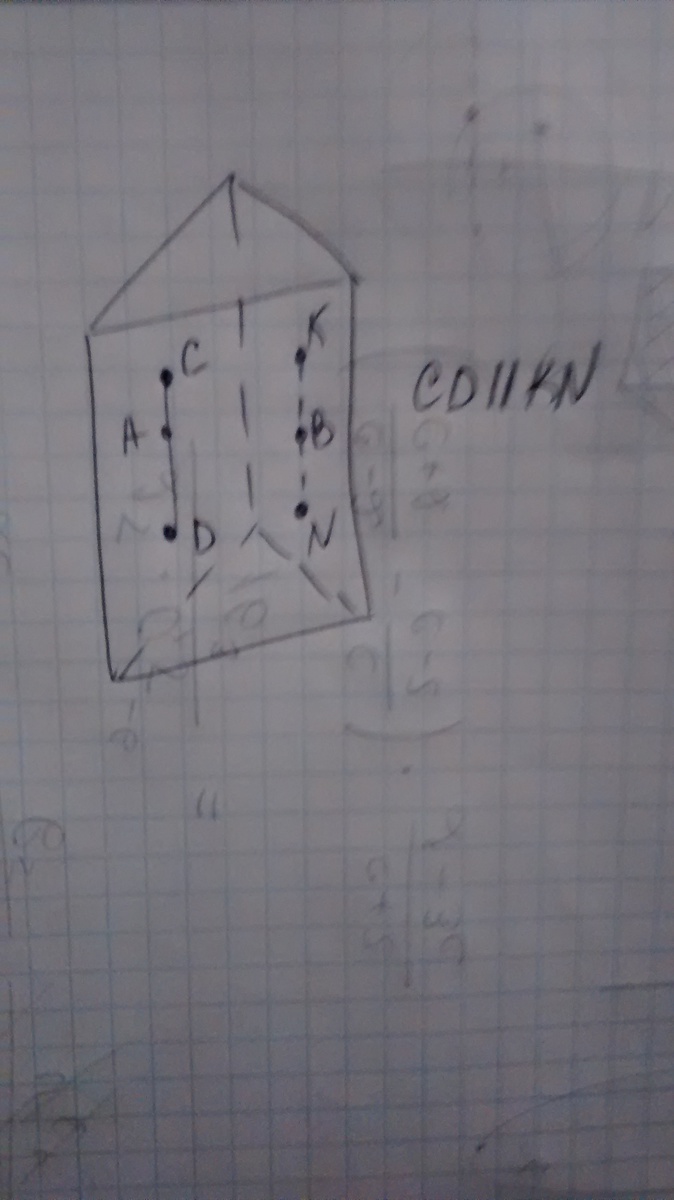
2. Точки A и B принадлежат смежным боковым граням призмы. Проведите в этих гранях через данные точки два отрезка, параллельные между собой.

Answer 1

1. а) Плоскости пересекаются по прямой с, следовательно прямая с принадлежит и плоскости α, и прямой β. Т. к. прямая а лежит в плоскости α, значит все ее точки лежат в плоскости α, и а пересекает β только в точке, которая принадлежит прямой с - общей для α и β.
б) Допустим, от противного, что прямая а пересекает с. Тогда точка пересечения будет принадлежать плоскости и α, и β. А сл-но, если у прямой и плоскости есть общая точка, то прямая пересекается эту плоскость, т. е. а пересекает β. По условию - противоречит. Значит а и с параллельны.

2. Рис.