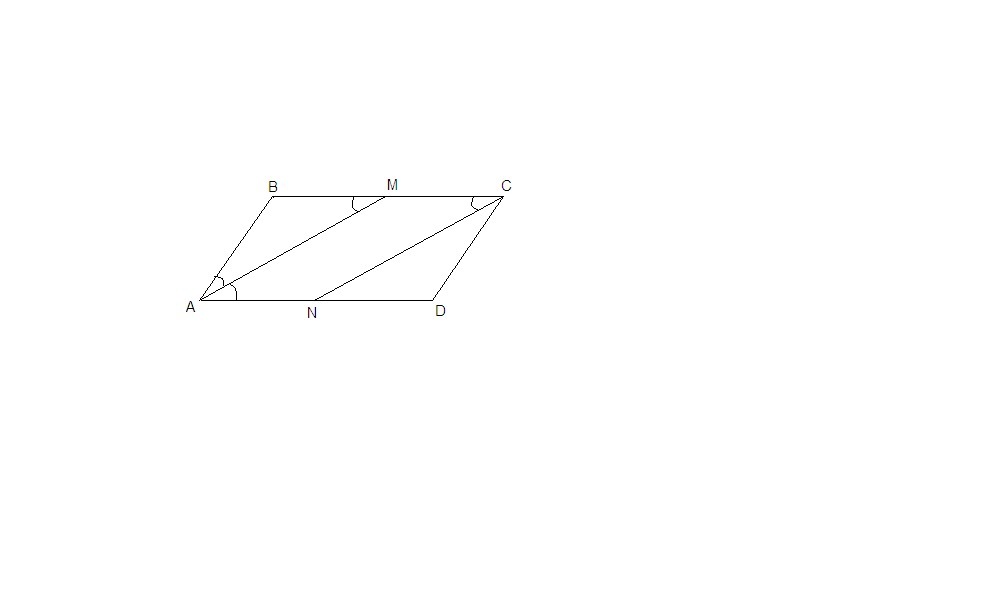
четырехугольник ABCD параллелограмм. луч AM биссектриса угла BAD, луч CN биссектриса угла BCD докажите что ANCM параллелограмм
Ответы
Ответ дал:
0
∠ВМА = ∠DAM как накрест лежащие при пересечении параллельных BC и AD секущей АМ.
∠DAM = ∠ВАМ так как АМ биссектриса, ⇒
∠ВАМ = ∠ВМА.
∠ВСN = ∠ВАМ как половины равных углов (противоположные углы параллелограмма равны), ⇒
∠BCN = ∠BMA, а это соответственные углы при пересечении прямых AM и CN секущей ВС, значит
AM║CN,
МС║AN, так как лежат на противоположных сторонах параллелограмма ABCD.
Если в четырехугольнике противолежащие стороны параллельны, то это параллелограмм.
∠DAM = ∠ВАМ так как АМ биссектриса, ⇒
∠ВАМ = ∠ВМА.
∠ВСN = ∠ВАМ как половины равных углов (противоположные углы параллелограмма равны), ⇒
∠BCN = ∠BMA, а это соответственные углы при пересечении прямых AM и CN секущей ВС, значит
AM║CN,
МС║AN, так как лежат на противоположных сторонах параллелограмма ABCD.
Если в четырехугольнике противолежащие стороны параллельны, то это параллелограмм.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад