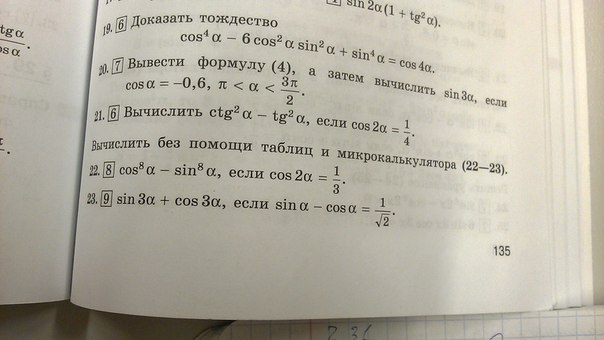Ответы
Ответ дал:
0
22)cos2a=1/3
 +
+
![[(1-cos2a)^2/4+(1+cos2a)^2/4]=cos2a*(1+2cos2a+coa^22a+1 [(1-cos2a)^2/4+(1+cos2a)^2/4]=cos2a*(1+2cos2a+coa^22a+1](https://tex.z-dn.net/?f=%5B%281-cos2a%29%5E2%2F4%2B%281%2Bcos2a%29%5E2%2F4%5D%3Dcos2a%2A%281%2B2cos2a%2Bcoa%5E22a%2B1) -
-

23)sina-cosa=1/√2
(sina-cosa)²=sin²a-2sinacosa+cos²a=1-sin2a=1/2⇒sin2a=1/2
cos2a=√1-sin²2a=√1-1/4=√3/2
sin²a=(1-cos2a)/2=(1-√3/2)/2=(2-√3)/4⇒sina=
cos²a=(1+cos2a)/2=(1+√3/2)/2=(2+√3)/4⇒cosa=
sin3a+cos3a=sin(2a+a)+cos(2a+a)=sin2acosa+cos2asina+cos2acosa-sin2asina=
=cosa(sin2a+cos2a)+sina(cos2a-sin2a)=
24)
10x=π/2+πn
x=π/20+πn/10
25)8sin2xcos2x=4
4sin4x=4
sin4x=1
4x=π/2+2πn
x=π/8+πn/2
23)sina-cosa=1/√2
(sina-cosa)²=sin²a-2sinacosa+cos²a=1-sin2a=1/2⇒sin2a=1/2
cos2a=√1-sin²2a=√1-1/4=√3/2
sin²a=(1-cos2a)/2=(1-√3/2)/2=(2-√3)/4⇒sina=
cos²a=(1+cos2a)/2=(1+√3/2)/2=(2+√3)/4⇒cosa=
sin3a+cos3a=sin(2a+a)+cos(2a+a)=sin2acosa+cos2asina+cos2acosa-sin2asina=
=cosa(sin2a+cos2a)+sina(cos2a-sin2a)=
24)
10x=π/2+πn
x=π/20+πn/10
25)8sin2xcos2x=4
4sin4x=4
sin4x=1
4x=π/2+2πn
x=π/8+πn/2
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад