Question

Один из углов равнобедренной трапеции равен 60 градусов а, диогональ  трапеции делит этот угол пополам.Найдите периметр трапеции ,если её большее основание  равно 14 см.

Answer 1

См. рис. 1
 угол 1 = углу 2 , так как диагональ биссектриса
   угол 2 = углу 3 как внутренние накрест лежащие.
  Значит угол 1 равен углу 3, треугольника равнобедренный и боковая сторона равна верхнему основанию
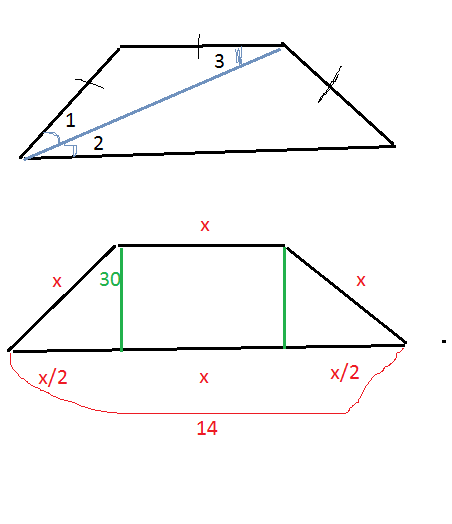
 См. рис. 2
Проведем высоты из вершин верхнего основания на нижнее.
 Получим два равных прямоугольных треугольника. Углы при основании трапеции 60°, значит второй угол прямоугольного треугольника 30°.
Против угла в 30° катет равен половине гипотенузы
х/2+х+х/2=14
2х=14
х=7
Р=7+7+7+14=35