Question

Стороны треугольника равны 51, 30 и 27 см. Из вершины меньшего угла треугольника проведен к его плоскости перпендикуляр длиной 10 см. Найдите расстояние от концов перпендикуляра до противолежащей стороны треугольника. C чертежом обязательно.

Answer 1

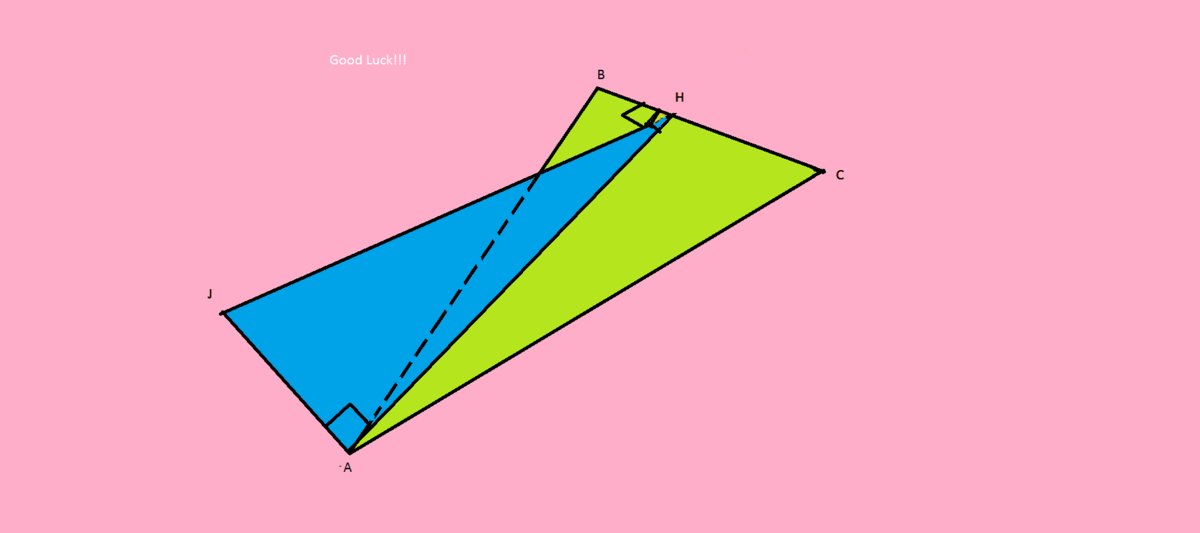
Пусть  JH искомое расстояние. JH перпендикулярно BC.
Поскольку JA перпендикулярна плоскости,то 
AH проекция  перпендикуляра JH на  плоскость.
Откуда по  теореме о 3  перпендикулярах: выходит  что  AH перпендикулярна BC,то  есть  высота треугольника ABC.
Меньший угол  всегда лежит против меньшей стороны ,то  есть напротив  стороны BC=27
Найдем площадь треугольника  по формуле Герона:
p=(51+30+27)/2=54
S=sqrt(54*3*24*27)=324
Откуда : раз S=AH*BC/2
AH=324*2/27=24
И  наконец  по теореме Пифагора:
JH^2=10^2+24^2=676=26^2
JH=26   Ответ: JH=26

Answer 2

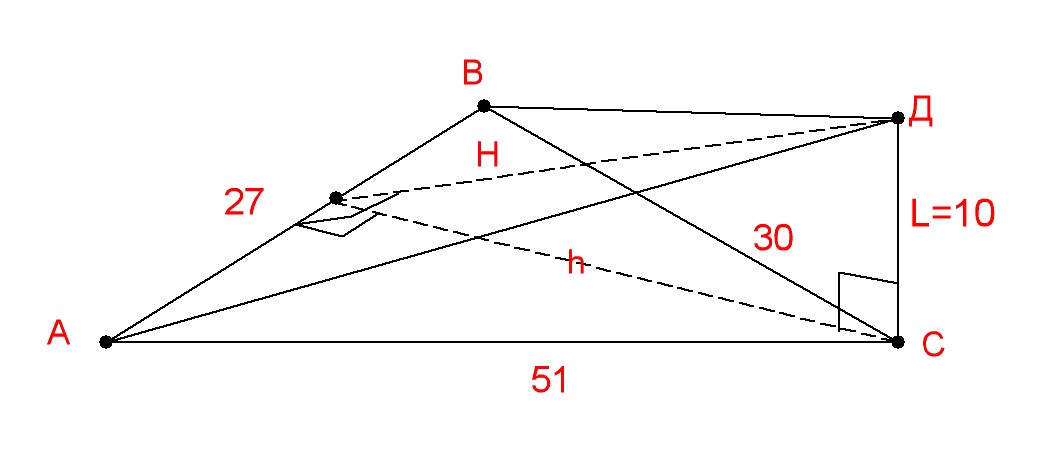
площадь треугольника АВС по формуле герона
S=корень(p*(p-a)*(p-b)*(p-c))= 324
расстояние от основания перпендикуляра до противоположной стороны h
S=h*a/2
h=2S/a=2*324/27=24
по теореме пифагора расстояние от конца перпендикуляра до противоположной стороны H = корень(h^2+L^2)=корень(24^2+10^2)=26