Через точку пересечения диагоналей квадрата проведены две взаимно перпендикулярные прямые .Докажите, что точки пересечения этих прямых со сторонами квадрата являются вершинами еще одного квадрата
Ответы
Ответ дал:
0
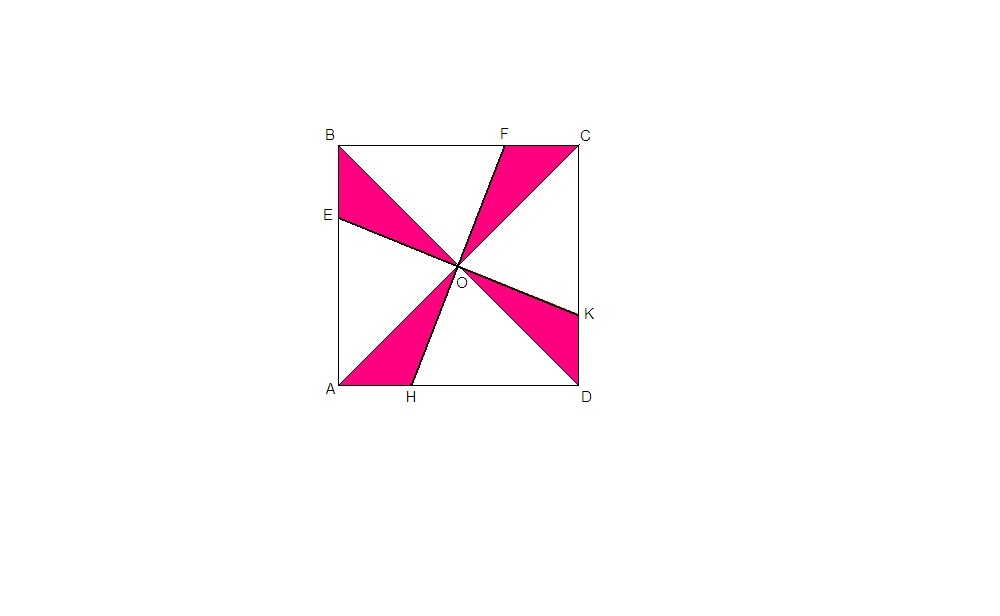
О - точка пересечения диагоналей квадрата ABCD.
EF⊥KH, EF∩KH = O
Розовые треугольники равны по гипотенузе и острому углу (гипотенузы - половинки равных диагоналей квадрата, угол 45°, так как в квадрате диагонали лежат на биссектрисах его углов)
Значит, OE = OF = OK = OH, и следовательно EF = KH.
Диагонали четырехугольника EFKH равны и точкой пересечения делятся пополам, значит это прямоугольник. А так как диагонали еще и перпендикулярны (по условию), то это квадрат.
EF⊥KH, EF∩KH = O
Розовые треугольники равны по гипотенузе и острому углу (гипотенузы - половинки равных диагоналей квадрата, угол 45°, так как в квадрате диагонали лежат на биссектрисах его углов)
Значит, OE = OF = OK = OH, и следовательно EF = KH.
Диагонали четырехугольника EFKH равны и точкой пересечения делятся пополам, значит это прямоугольник. А так как диагонали еще и перпендикулярны (по условию), то это квадрат.
Приложения:
Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад