Question

Помогите решить, пожалуйста!
1. В кубе ABCDA1B1C1D1 длина ребра равна 1. M - центр грани DD1C1C. Используя метод координат, найдите:
1) Угол между прямыми AM и B1D
2) Расстояние между серединами отрезков AM и B1D.
2. Даны две точки: A, лежащая на оси ординат, и B (1; 0; 1). Прямая AB составляет с плоскостью OXZ угол 30 градусов. Найдите координаты точки A.
3. Найдите координаты вектора а, коллинеарного вектору b {6; 8 - 7,5} и образующего тупой угол с координатным вектором j, если модуль вектора a IaI=50.

Answer 1

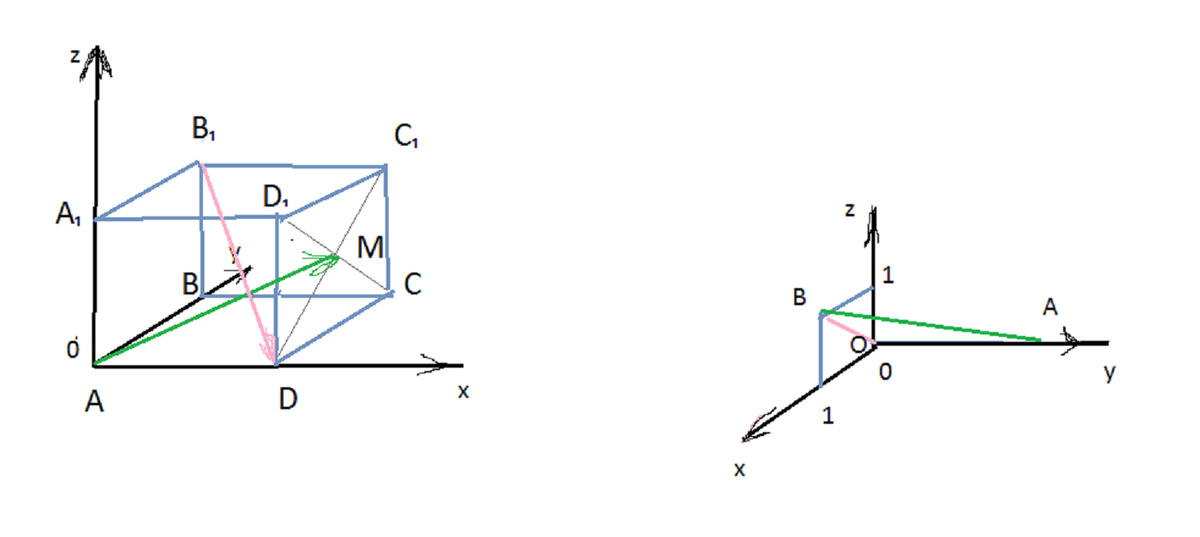
1) Расположим куб в системе координат так, как показано на рисунке. Точка А - совпадаем с началом координат. Тогда координаты  вершин
А(0;0;0) ;  В(0;1:0) ;  С(1; 1; 0)  ;   D(1; 0; 0) ;  В₁(0;1;1)
Координаты точки М (1; 1/2; 1/2)
Координаты векторов
$overrightarrow{AM}=(1; frac{1}{2}; frac{1}{2} ), \ overrightarrow{B _{1}D }=(1-0;0-1;0-1)=(1;-1;-1) \ overrightarrow{AM}cdot overrightarrow{B _{1}D} =1cdot1+ frac{1}{2}cdot(-1)+ frac{1}{2}cdot(-1)=0$   
Скалярное произведение равно 0, значит векторы ортогональны, прямые AM и B₁D перпендикулярны
Найдем координаты середины отрезка В₁D  - точки  K
$x _{K}= frac{x_B _{1}+x_D }{2}= frac{0+1}{2}= frac{1}{2}, \ y _{K}= frac{y_B _{1}+y_D }{2}= frac{1+0}{2}= frac{1}{2}, \ z _{K}= frac{z_B _{1}+z_D }{2}= frac{0+1}{2}= frac{1}{2}.$
K(1/2; 1/2;1/2)
Найдем координаты середины отрезка АМ - точки Е
$x _{E}= frac{x_A +x_M }{2}= frac{0+1}{2}= frac{1}{2}, \ y _{E}= frac{y_A +y_M }{2}= frac{1+ frac{1}{2} }{2}= frac{1}{4}, \ z _{E}= frac{z_A+z_M }{2}= frac{0+ frac{1}{2} }{2}= frac{1}{4}.$
E=(1/2; 1/4:1/4)
$EK= sqrt{(x_K-x_E) ^{2}+(y_K-y_E) ^{2} +(z_K-z_E) ^{2}} = \ =sqrt{( frac{1}{2} - frac{1}{2} ) ^{2}+( frac{1}{2} - frac{1}{4} ) ^{2} +( frac{1}{2} - frac{1}{4} ) ^{2}}= sqrt {0+ frac{1}{16}+frac{1}{16} }= sqrt{ frac{1}{8} }= frac{1}{2 sqrt{2} }= \ = frac{ sqrt{2} }{4}$
Ответ. 1) прямые АМ и В₁D перпендикулярны, угол между ними 90°.2) расстояние между серединами отрезков АМ и В₁D  равно$frac{ sqrt{2} }{4}$

Задача 2. ( см. рис. 2)
В грани ОХZ - квадрат, все стороны которого 1. Диагональ квадрата ОВ имеет длину √2 и легко находится по теореме Пифагора 1²+1²=2²
В прямоугольном треугольнике АВО  угол АВО равен 30°, угол АОВ равен 90°, так как ось оу перпендикулярна плоскости ОХZ.
В прямоугольном треугольнике против угла в 30° катет в два раза меньше гипотенузы. Пусть ОА=y, тогда АВ=2y
По теореме Пифагора АВ²=АО²+ВО²
(2y)²=y²+(√2)²  ⇒  3y²=2    ⇒$y^{2} = frac{2}{3}Rightarrow y= sqrt{ frac{2}{3} }$
Ответ.$A( sqrt{ frac{2}{3} };0;0)$

Задача 3.
Так как векторы а и b коллинеарны, то их координаты пропорциональны.
Вектор a  имеет координаты (6k; 8k;-7,5k), где k- коэффициента пропорциональности
Так как угол между векторами a   и j  -  тупой, значит их скалярное произведение отрицательно.
Координаты вектора j  - (0;1:0)
Найдем скалярное произведение
$overrightarrow{a}cdot overrightarrow{j}=6kcdot0+8kcdot1+(-7,5k)cdot0=8k<0, \k<0\ |overrightarrow{a}|=50, \ sqrt{(6k) ^{2} +(8k) ^{2}+(-7,5k) ^{2} }=50, \ sqrt{156,25k ^{2} }=50, \156,25k ^{2}=2500 \ k ^{2}= frac{2500}{156,25} =4$
Так как k<0, то к=-2
Ответ. Вектор a    имеет координаты (6·(-2); 8·(-2);-7,5·(-2)=(-12; -16; 15)

Answer 2

Очень прошу не размещать три больших задачи в одном вопросе. Пока набирала, появилась строчка, что время для ответа истекло и соединение будет прервано. Хорошо, что успела скопировать такое огромное решение.

Answer 3

Хорошо. Спасибо огромное!