Крч высшая матика. Матрицы:
1.Вычислить и определить:
![left[begin{array}{ccc}1&5&8\2&7&1\1&1&2end{array}right] left[begin{array}{ccc}1&5&8\2&7&1\1&1&2end{array}right]](https://tex.z-dn.net/?f=+left%5Bbegin%7Barray%7D%7Bccc%7D1%26amp%3B5%26amp%3B8%5C2%26amp%3B7%26amp%3B1%5C1%26amp%3B1%26amp%3B2end%7Barray%7Dright%5D+)
2.Найти матрицу, обратную данной:
![left[begin{array}{ccc}2&3&4\1&2&3\1&3&6end{array}right] left[begin{array}{ccc}2&3&4\1&2&3\1&3&6end{array}right]](https://tex.z-dn.net/?f=+left%5Bbegin%7Barray%7D%7Bccc%7D2%26amp%3B3%26amp%3B4%5C1%26amp%3B2%26amp%3B3%5C1%26amp%3B3%26amp%3B6end%7Barray%7Dright%5D+)
3.Решить систему уравнений двумя методами:
{ x -2y +z = 7
{ 2x -3y -5z = -8
{ 4x +5y -z = 0
Ответы
Ответ дал:
0
Как М - матрицу миноров соответствующих элементов матрицы В нашли, см. в прикр. файле
Приложения:
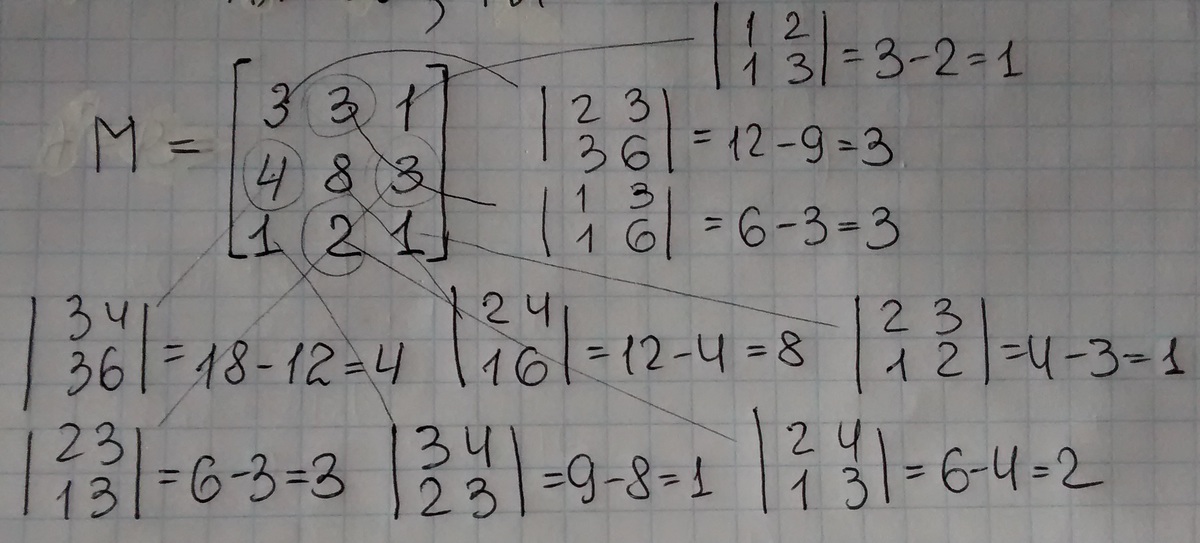

Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад