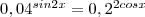Question

найти корни на промежутке [7pi/2;9pi/2]

Answer 1

$0,2^{2sin2x} = 0,2^{2cosx}$
2sin2x=2cosx
2sinxcosx-cosx=0
cosx(2sinx-1)=0
cosx=0⇒x=π/2+πn
n=3  x=π/2+3π=7π/2∈[7π/2;9π/2]
n=4  x=π/2+4π=9π/2∈[7π/2;9π/2]
sinx=1/2⇒x=(-1)^n*π/6+πn
n=4  x=25π/6∈[7π/2;9π/2]

Answer 2

13п/6 не входит!!!!!!!!!!!!

Answer 3

$0.04^{sin2x}=0.2^{2cos x} \ \ 0.2^{2sin2x}=0.2^{2cos x} \ sin2x=cos x \ 2sin xcdotcos x-cos x=0 \ cos x(2sin x-1)=0 \ cos x=0 \ x= frac{ pi }{2}+ pi n, n in Z \ sin x= frac{1}{2} \ x=(-1)^kcdot frac{ pi }{6} + pi k, k in Z$

Корни для x = π/2 + πn
n = 3; x=π/2+3π=π/2+6π/2=7π/2
n = 4; x=π/2+4π=π/2+8π/2=9π/2
Корни для (-1)^k * π/6 + πk
k = 4; x= 25π/6