Задано трикутника ABC і точку М поза його площиною, МА=а, МС=с, СВ=в. Знайдіть розкладання вектора МD за векторами а, в, с де точка D - середина сторони АВ.
Ответы
Ответ дал:
0
Тут  не знадобиться.
не знадобиться.
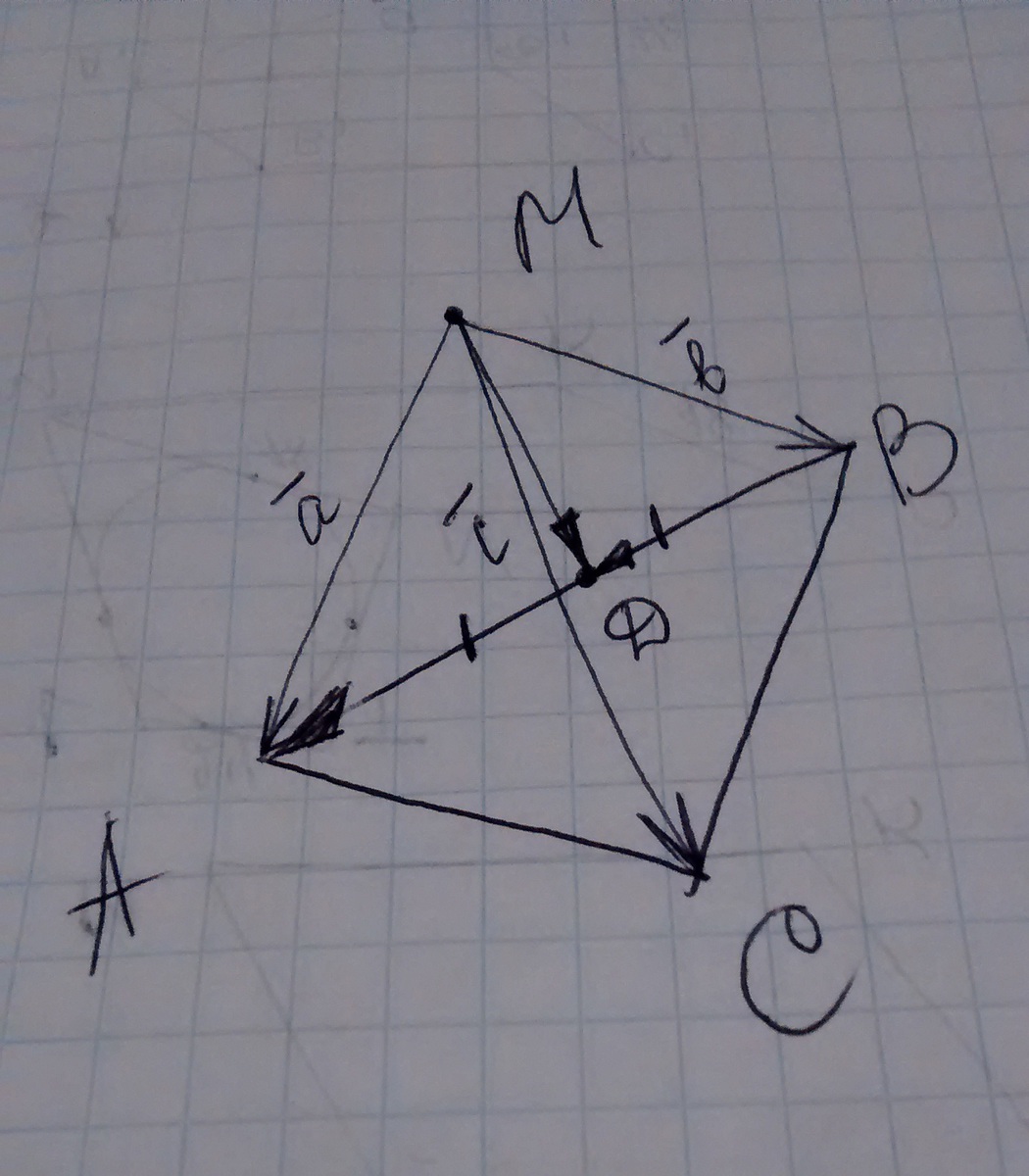
Дивись рисунок до задачі у прикріпленому файлі.
За правилом трикутника додавання векторів, виразимо через
через  .
.

Дивись рисунок до задачі у прикріпленому файлі.
За правилом трикутника додавання векторів, виразимо
Приложения:

Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад