Лодка по течению реки проходит 12 км на
30мин быстрее, чем такое же расстояние против течения реки. Найди
собственную скорость лодки, если скорость течения реки 2км/ч.
Ответы
Ответ дал:
0
Пусть собственная скорость лодки x км/ч, тогда по течению скорость будет x+2, а против х-2.

Времени затратил больше на дорогу при обратном движении, против течения, следовательно

Cкорость отрицательной быть не может, следовательно х=10 км/ч - собственная скорость лодки.
Времени затратил больше на дорогу при обратном движении, против течения, следовательно
Cкорость отрицательной быть не может, следовательно х=10 км/ч - собственная скорость лодки.
Приложения:
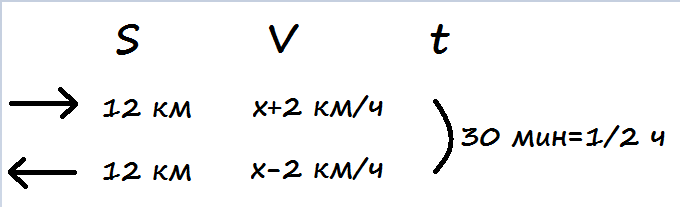

Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад