Помогите решить неравенство!!!!!!!!!!!!!!!!!!!3-соs x меньше или равно x(в четвертой степени)+6x во второй степени+13
Ответы
Ответ дал:
0
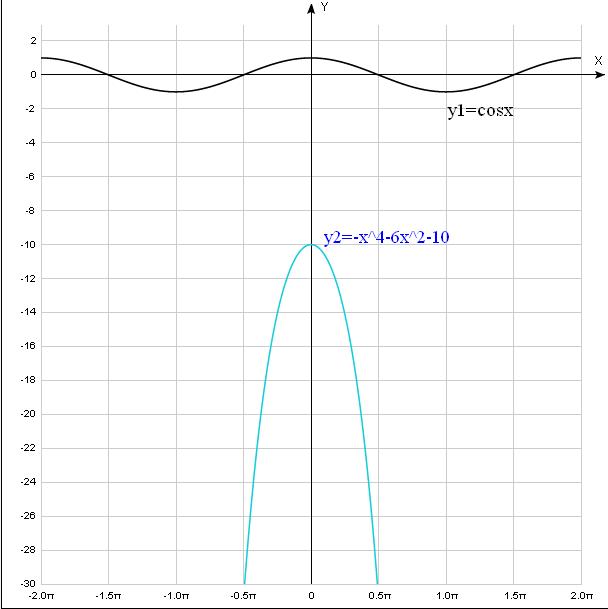
Решим графически:
Функция косинуса - известная функция.
Для построения функции
1) Нули функции:
2)
3) Точки максимума и минимума:
4) Функция возрастает при x<0, убывает при x>0.
По рисунку видно, что график функции
Ответ: х - любое число (x∈R)
Приложения:
Ответ дал:
0
Спасибо огромное!Вы очень помогли:)
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад