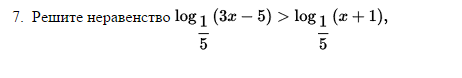Ответы
Ответ дал:
0
Log ( 3X-5 ) > Log(X+1)
Допустимыми значениями является объединие промежутков : X > 5/3 и X > -1 .
Значит X > 5/3 .
Log ( 3X-5 ) - Log(X+1) > 0
Log 1 = 0
Log ( 3X-5 ) - Log(X+1) > Log ( 1 )
Log[ ( 3X-5 ) / (X+1) ] > Log 1
Везде основание логарифма равно 1 / 5 = 0,2 .
0 < 0,2 < 1, значит функция Log( X ) ,будет убывающей !
При переходе от Log к неравенству следует поменять его знак !
Далее : ( 3X-5 ) / ( X+1) < 1
3X-5 < X+1
X < 3
Искомым решением неравенства будет являться промежуток ( 5/3 ; 3 ) ...
Пожалуйста, проверьте ...
Допустимыми значениями является объединие промежутков : X > 5/3 и X > -1 .
Значит X > 5/3 .
Log ( 3X-5 ) - Log(X+1) > 0
Log 1 = 0
Log ( 3X-5 ) - Log(X+1) > Log ( 1 )
Log[ ( 3X-5 ) / (X+1) ] > Log 1
Везде основание логарифма равно 1 / 5 = 0,2 .
0 < 0,2 < 1, значит функция Log( X ) ,будет убывающей !
При переходе от Log к неравенству следует поменять его знак !
Далее : ( 3X-5 ) / ( X+1) < 1
3X-5 < X+1
X < 3
Искомым решением неравенства будет являться промежуток ( 5/3 ; 3 ) ...
Пожалуйста, проверьте ...
Ответ дал:
0
не
Ответ дал:
0
не то
Ответ дал:
0
убери))
Ответ дал:
0
ОДЗ
3x-5>0
x+1>0
x>5/3
x>-1
x>5/3
Log(1/5)(3x-5)>log(1/5)(x+1)т.к. 1/5 <1 , значит
3x-5<x+1
x<3
c учетом ОДЗ
5/3<x<3
3x-5>0
x+1>0
x>5/3
x>-1
x>5/3
Log(1/5)(3x-5)>log(1/5)(x+1)т.к. 1/5 <1 , значит
3x-5<x+1
x<3
c учетом ОДЗ
5/3<x<3
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад