Question

Биссектрисы угла B и угла C параллелограмма ABCD пересекаются в точке, лежащей на стороне Ad. найдите стороны параллелограмма, если его P=20см

Answer 1

По свойству биссектрис соседних углов нужно заметить,что они пересекаются на бОльшей стороне  параллелограмма только в том случае,если бОльшая сторона больше меньшей ровно в два раза. А т.к. у нас две биссектрисы пересекаются на стороне АД( большей),то АД больше АВ ВДВОЕ. .имеем уравнение 
пусть АВ- Хсм( и равна  СД),тогда тогда АД 2Х (и равна ВС)
Х+Х+2Х+2Х=20
6х=20
Х=3,3
сторона АВ=СД=3,33 СМ
сторонаВС= АД=6,66 СМ

Answer 2

Вариант ответа. 
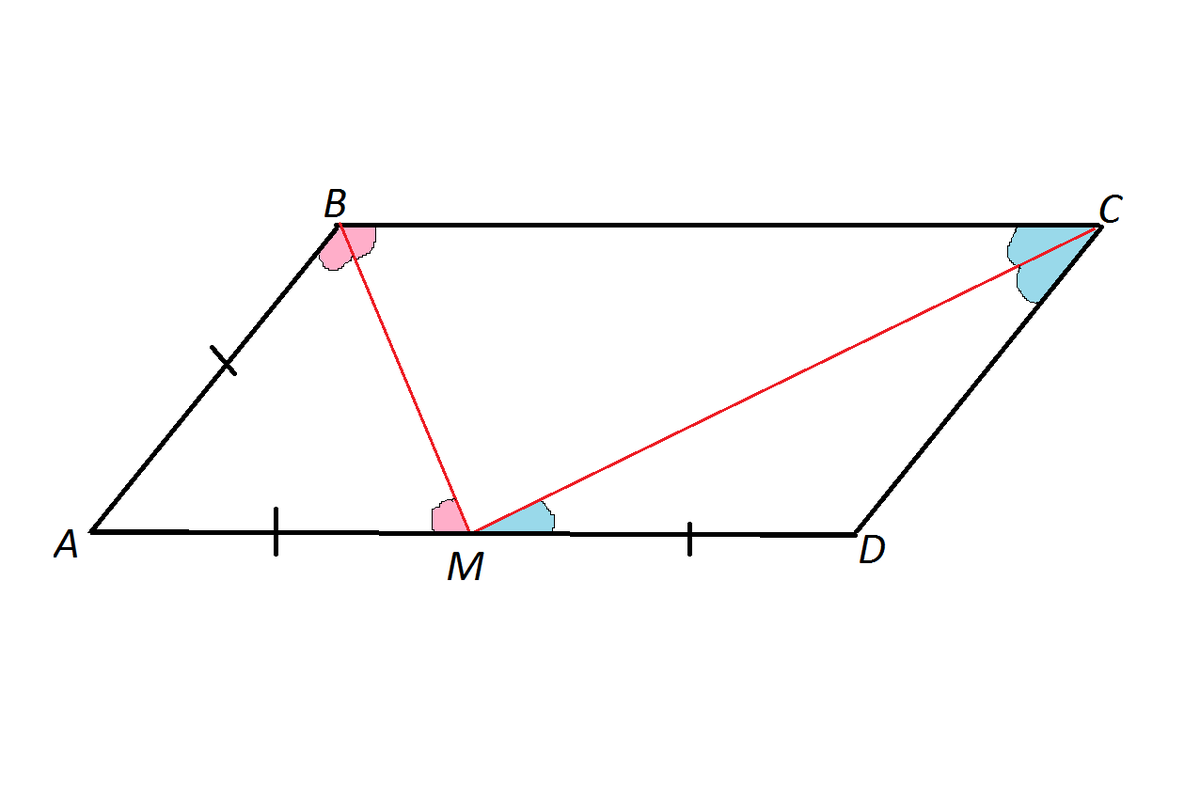
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
В самом деле, углы СВМ и ВМА  равны как накрестлежащие при пересечении параллельных прямых секущей.
Но∠СВМ равен углу АВМ ⇒∠АВМ=∠ВМА, и
 треугольник АВМ - равнобедренный.
АВ=АМ
На том же основании МD=СD
А так как АВ=СD, то АD=BC=АМ+МD= 2 АВ
Р (АВСD)=2·(АВ+АD)=2·(АВ+2 АВ)=6 АВ
6 АВ=20
АВ=20:6=3 ¹/₃ см
АD=6 ²/₃ см