Question

постройте график прямой пропорциональности, заданной формулой:
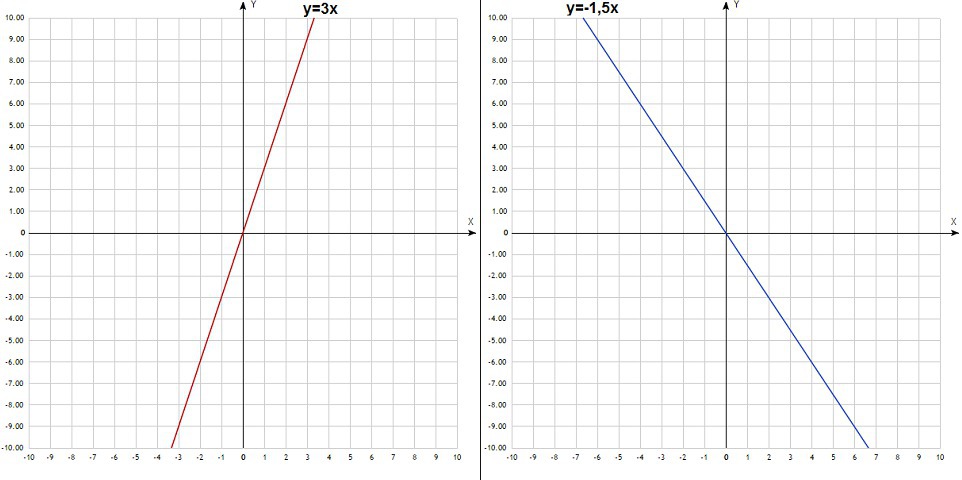
y=3x
y=-1,5x
y=x
y=-x
y=2,5x
y=-4,5x

Answer 1

Графики во вложении.
Все функции в условии, являются уравнениями чей график - обычная прямая. Так как они имеют вид:
$y=ax+b$ - a угловой коэффициент,b точка пересечения прямой с осью у.

У каждой прямой $b=0$, следовательно, данные прямые пересекают ось у в начале координат.
А так же ось х в начале координат. Так как:
$0=ax\x=0$

Это прямые, а значит:
$D(y)=(-infty,+infty)$ - область определения.
$E(y)=(-infty,+infty)$ - область значений.

Теперь, по отдельности строим каждый график:
1. 
$y=3x$

Здесь $a=3 Rightarrow 3 textgreater 0$, следовательно, данная функция всегда возрастает.
Нуль функции:
$y=0 Rightarrow (0,0)$

Знак функции:
$f(x) geq 0 rightarrow xin[0,+infty)$
$f(x) textless 0 rightarrow xin (-infty,0)$

2. 
$y=-1,5x$

Здесь  $a=-1,5x Rightarrow -1,5 textless 0$ следовательно, данная функция всегда убывает.
Нуль функции:
$y=0 Rightarrow (0,0)$

Знак функции:
$f(x) geq 0 rightarrow xin(-infty,0]$
$f(x) textless 0 rightarrow xin(0,+infty)$

3.
$y=x$

Здесь $a=1 Rightarrow 1 textgreater 0$, следовательно, данная функция всегда возрастает.
Нуль функции:
$y=0 Rightarrow (0,0)$

Знак функции:
$f(x) geq 0 rightarrow xin(-infty,0]$
$f(x) textless 0 rightarrow xin(0,+infty)$

4.
$y=-x$

Здесь  $a=-1x Rightarrow -1 textless 0$ следовательно, данная функция всегда убывает.
Нуль функции:
$y=0 Rightarrow (0,0)$

Знак функции:
$f(x) geq 0 rightarrow xin(-infty,0]$
$f(x) textless 0 rightarrow xin(0,+infty)$

5.
$y=2,5x$

Здесь $a=2,5Rightarrow 2,5 textgreater 0$, следовательно, данная функция всегда возрастает.
Нуль функции:
$y=0 Rightarrow (0,0)$

Знак функции:
$f(x) geq 0 rightarrow xin(-infty,0]$
$f(x) textless 0 rightarrow xin(0,+infty)$

6.
$y=-4,5x$

Здесь  $a=-4,5x Rightarrow -4,5 textless 0$ следовательно, данная функция всегда убывает.
Нуль функции:
$y=0 Rightarrow (0,0)$

Знак функции:
$f(x) geq 0 rightarrow xin(-infty,0]$
$f(x) textless 0 rightarrow xin(0,+infty)$