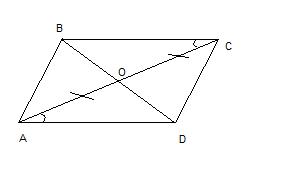
Отрезки ac и bd пересекаются в середине O отрезка AC, угол BCO = углу DAO. Докажите, что треугольник BOA= треугольнику DOC
Ответы
Ответ дал:
0
Углы ВСО и DAO - накрест лежащие углы при пересечении двух прямых ВС и AD секущей АС. По условию они равны, значит, ВС II AD.
Треугольники ВОС и DOA равны по стороне и двум прилежащим к ней углам (второй признак равенства треуг-ов):
- <BCO=<DAO по условию;
- <BOC=<DOA как вертикальные углы;
- АО=СО по условию.
У равных треугольников равны и соответственные стороны ВО и DO.
Рассмотрим треуг-ки ВОА и DOC. Они равны по двум сторонам и углу между ними (первый признак равенства треуг-ов):
- ВО=DO как только что доказано;
- АО=СО по условию;
- углы ВОА и DОС равны как вертикальные.
Треугольники ВОС и DOA равны по стороне и двум прилежащим к ней углам (второй признак равенства треуг-ов):
- <BCO=<DAO по условию;
- <BOC=<DOA как вертикальные углы;
- АО=СО по условию.
У равных треугольников равны и соответственные стороны ВО и DO.
Рассмотрим треуг-ки ВОА и DOC. Они равны по двум сторонам и углу между ними (первый признак равенства треуг-ов):
- ВО=DO как только что доказано;
- АО=СО по условию;
- углы ВОА и DОС равны как вертикальные.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад