355 - 1 - 3,5
356 - 1 - 3
357 - 1
359 - 1 - 3
Решите красиво системой напишите через вставить и редактировать уравнение или на листике - через одз подробно - решайте х больше 5 х+5 больше 0 и log5(x+2)меньше(это знаком) log 3 81 - это например и т.д. таким способом системой .
Приложения:
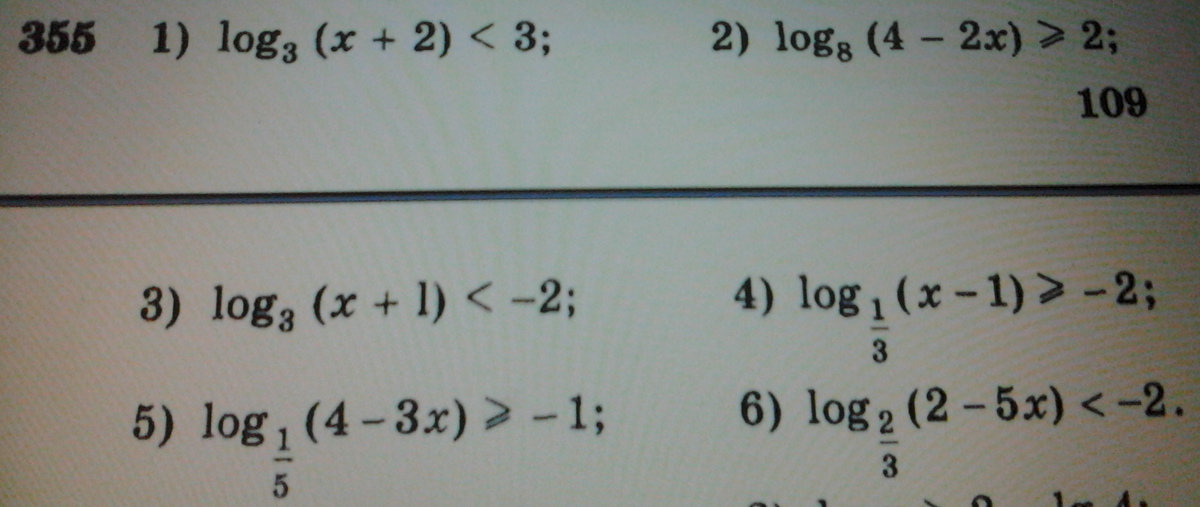
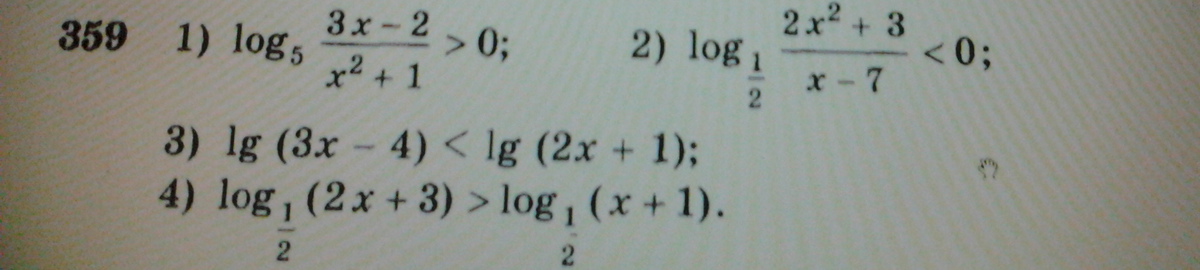
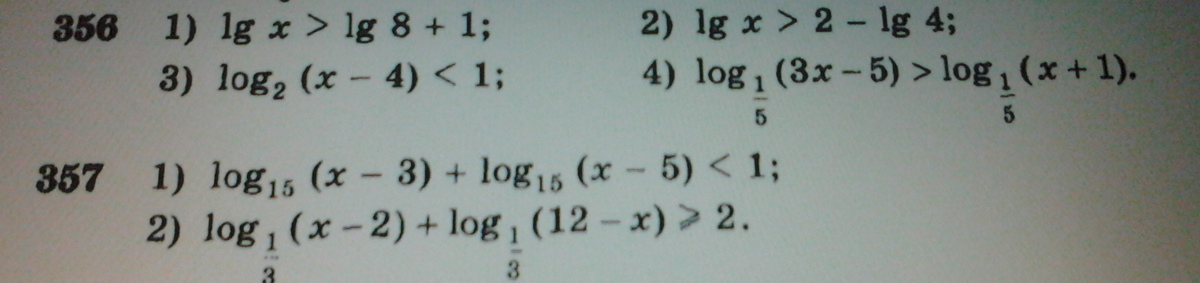
Ответы
Ответ дал:
0
355

ОДЗ: x+2>0 ⇒ x>-2

Так как 3>1, то функция возрастающая, знак неравества сохраняется

Ответ: (-2;25)

ОДЗ: x+1>0 ⇒ x>-1
3>1, функция возрастающая, знак неравенства не меняется

Ответ:

ОДЗ: 4-3x>0 ⇒ x<4/3
1/5<1, функция убывающая, знак неравенства меняется на противоположный

Ответ:
356

ОДЗ: x>0

Ответ:

ОДЗ: x-4>0⇒ x>4

Ответ:
357

ОДЗ:

___+___(0)__-___(8)____+____> ⇔x ∈ (0;8)
Ответ: x ∈ (5;8)
359

ОДЗ: 3x-2>0 ⇔ x>2/3

Ответ:x>2/3

ОДЗ:

Ответ:
ОДЗ: x+2>0 ⇒ x>-2
Так как 3>1, то функция возрастающая, знак неравества сохраняется
Ответ: (-2;25)
ОДЗ: x+1>0 ⇒ x>-1
3>1, функция возрастающая, знак неравенства не меняется
Ответ:
ОДЗ: 4-3x>0 ⇒ x<4/3
1/5<1, функция убывающая, знак неравенства меняется на противоположный
Ответ:
356
ОДЗ: x>0
Ответ:
ОДЗ: x-4>0⇒ x>4
Ответ:
357
ОДЗ:
___+___(0)__-___(8)____+____> ⇔x ∈ (0;8)
Ответ: x ∈ (5;8)
359
ОДЗ: 3x-2>0 ⇔ x>2/3
Ответ:x>2/3
ОДЗ:
Ответ:
Ответ дал:
0
359-1,ошибка...после одз...вы не записали решения...а ведь их там и нет(подставьте любое х,а значение будет больше 0...
Ответ дал:
0
а хотя стоп...
Ответ дал:
0
все норм,извиняюсь
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад