Найти предел, не используя правило Лопиталя:
предел дроби (х+3)/(х+4) в степени (-2х), где х стремится к бесконечности

Ответы
Ответ дал:
0
Приложения:
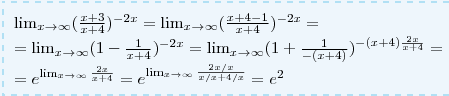
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад