Question

Острый угол прямоугольного треугольника равен 75°. Найдите угол между высотой и медианой, проведенных из высоты

Answer 1

191. Острый угол прямоугольного треугольника равен 75°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла.

Пусть дан треугольник АВС. угол С=90°, угол АВС=75°.

Сумма острых углов прямоугольного треугольника 90°. 

⇒ угол ВАС=90°-75°=15°

Медиана прямоугольного треугольника, проведенная из прямого угла,  равна половине гипотенузы.

АМ=СМ и  СМ=ВМ. Треугольники АМС и ВМС равнобедренные с основаниями АС и ВС соответственно. 

∠МСА=∠САМ=15°

∠ВСМ=∠СВМ=75°

В прямоугольном ∆ ВСН острый угол ВСН=90°-75°=15°

Угол НСМ= ∠ВСМ-∠ВСН=75°-15°°=60°

----------

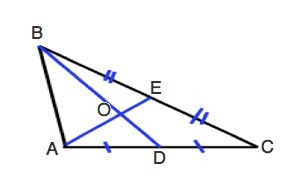
192.  Дано: ∆ АВС. 

СЕ=ВЕ; AD=DC

OE+OD=5

Найдите: АЕ+BD. 

Точки Е и D делят стороны, на которых лежат. пополам. Следовательно, ВD и АЕ - медианы. 

Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. 

⇒ ОЕ=АЕ/3,  OD=BD/3

 АЕ/3+BD/3=5

⇒ AE+BD=3•5=15