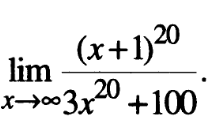Ответы
Ответ дал:
0
Выносим x^20 в числителе и в знаменателе, в числителе получим нечто вида
x^20(1 + ax + bx^2 + ...... 1x^20), а в знаменателе - x^20(3 + 100x^20)
сокращаем на x^20, подставляем предел, все слагаемые вида 1х^a уходят в ноль, остается 13.
Для подобных пределов, когда x стремится к бесконечности есть общее правило, что предел равен отношению коэффициентов при старших степенях в случае, если степени числителя и знаменателя совпадают.
x^20(1 + ax + bx^2 + ...... 1x^20), а в знаменателе - x^20(3 + 100x^20)
сокращаем на x^20, подставляем предел, все слагаемые вида 1х^a уходят в ноль, остается 13.
Для подобных пределов, когда x стремится к бесконечности есть общее правило, что предел равен отношению коэффициентов при старших степенях в случае, если степени числителя и знаменателя совпадают.
Ответ дал:
0
а почему в числителе получится x^20(1 + ax + bx^2 + ...... 1x^20)?
Ответ дал:
0
большое спасибо
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад