Дан параллелепипед ABCDA1B1C1D1.Постройте сечение параллелепипеда плоскостью проходящей через середину ребра АВ||плоскости DBB1.
Друзья помогите с решением задачи,пожалуйста))Очень нужно
Ответы
Ответ дал:
0
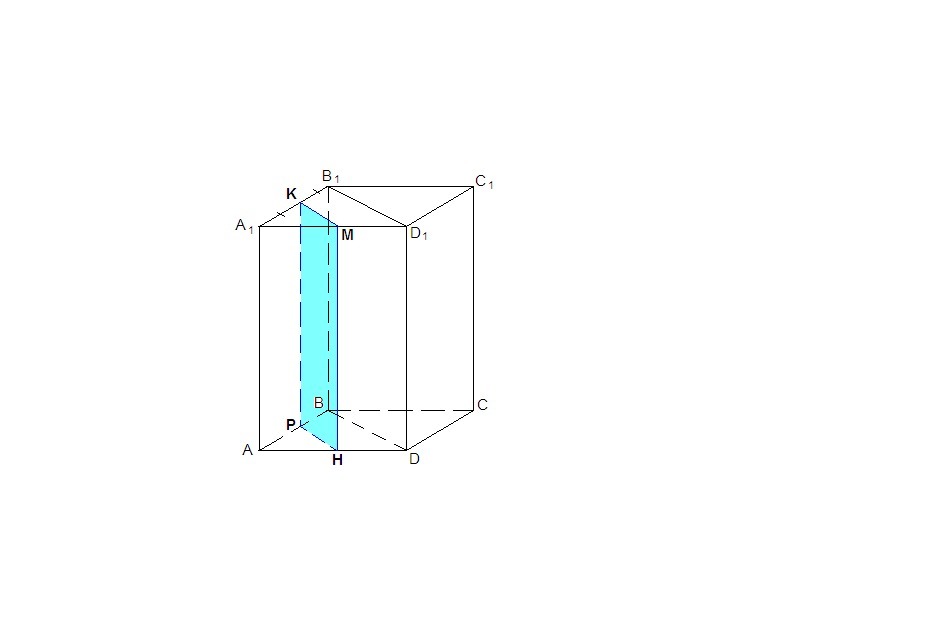
Пусть Р - середина ребра АВ, а Н - середина ребра AD.
Проведем РН. РН ║BD как средняя линия треугольника ABD.
Проведем РК║ВВ₁ и МН║DD₁.
Соединим точки К и М.
РКМН - искомое сечение.
Доказательство:
- сечение проходит через точку Р;
- РН║BD и РК║ВВ₁, а если две пересекающиеся прямы одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны, значит
РКМ║DBB₁.
Приложения:
Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад