Даю 30 балов!
Построить график функции y=2/x
1) Найдите область определения функции.
2) Какие значения принимает функция.
3) Укажите промежутки возрастания(убывания) функции.
4) Укажите промежутки, в которых функция принимает положительные и отрицательные значения.
Ответы
Ответ дал:
0
Знаменатель не может быть равен нулю (на ноль делить нельзя)


3) Найдём производную по правилу
и формулам

Приравняем к нулю.

— ч —
---------------o-------------->x
0
Функция убывает на промежутке
4)
— +
----------------o------------->x
0
Функция принимает положительные значения на промежутке
Функция принимает отрицательные значения на промежутке
3) Найдём производную по правилу
и формулам
Приравняем к нулю.
— ч —
---------------o-------------->x
0
Функция убывает на промежутке
4)
— +
----------------o------------->x
0
Функция принимает положительные значения на промежутке
Функция принимает отрицательные значения на промежутке
Приложения:
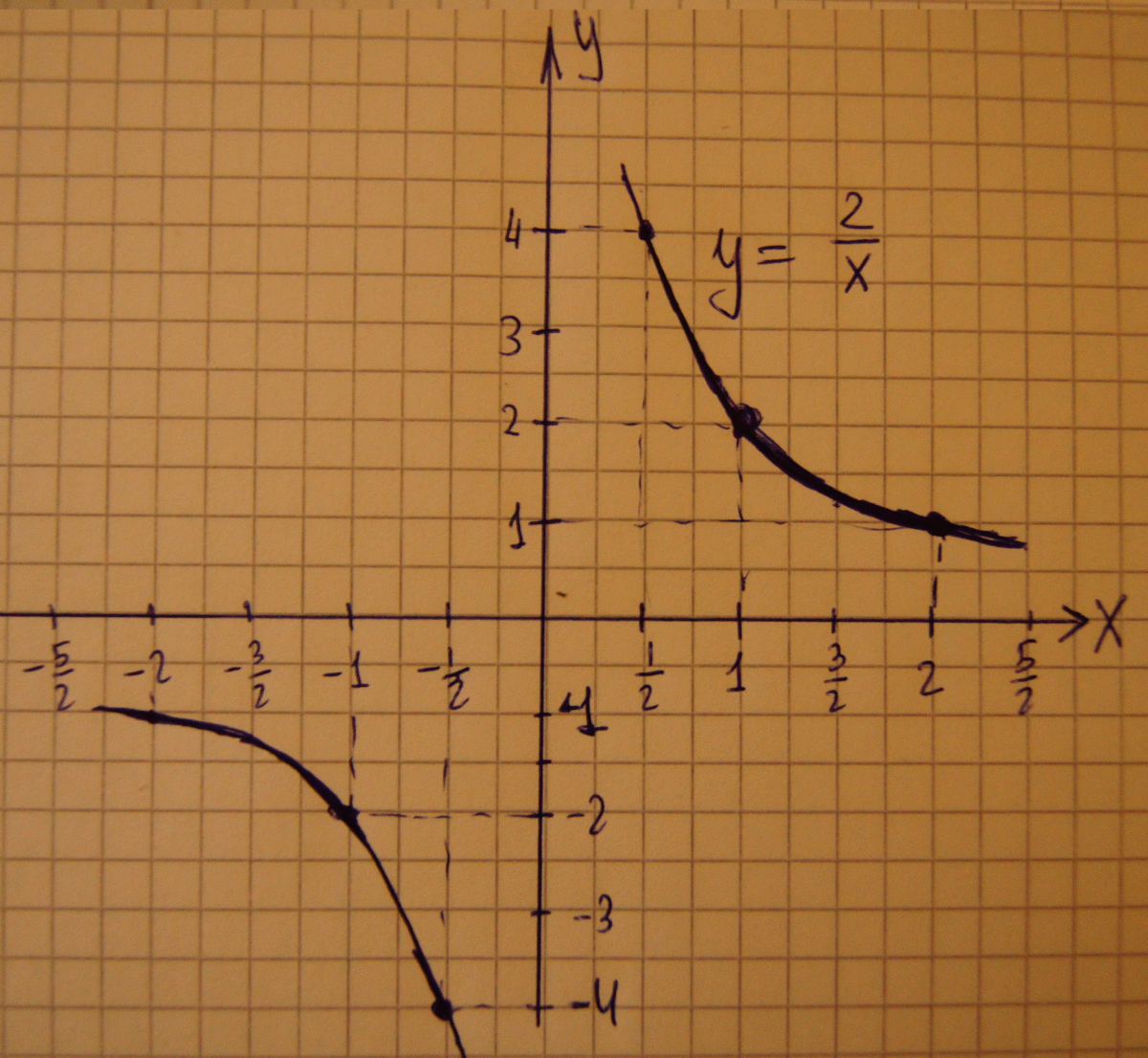
Ответ дал:
0
Смотреть во вложении
Приложения:

Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад