Составить уравнение геометрического места точек, отношение расстояний до данной точки А(1;4) и прямой х=1/2 равна числу Е=0,8. Полученное уравнение привести к простейшему виду и построить кривую,отметить на рисунке фокальные точки и директрисы
Ответы
Ответ дал:
0
Пусть точка M(x,y) - любая произвольная точка искомой кривой. тогда расстояние от точки A(1,4) до любой точки искомой кривой можно найти по формуле:
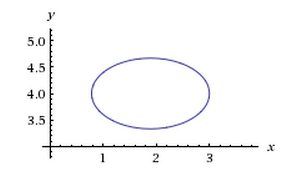
Это уравнение эллипса, О(17/9;4), а=1, b=0,6
Эксцентриситет
Фокальный параметр
Директрисса
Приложения:
Ответ дал:
0
исправь пожалуйста ошибку
Ответ дал:
0
Я не могу исправить ошибку, когда пометили "как нарушение". Попроси одного из модераторов снять и позволить редактирование, тогда смогу исправить, или создай заново задание. Странно, что еще не удалили это решение
Ответ дал:
0
http://znanija.com/task/9028137
Ответ дал:
0
Мне дали отредактировать, см. выше
Ответ дал:
0
ок
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад