Question

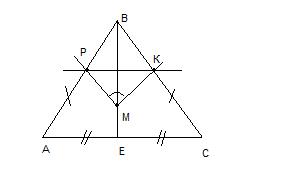
В треугольнике АВС АВ= ВС. На медиане ВЕ отмечена точка М, а на сторонах АВ и ВС-точки Р и К соответственно. (Точки Р, М и К не лежат на одной прямой.)
Известно, что угол ВМР=ВМК. Докажите, что:
Прямые РК и ВМ взаимно перпендикулярны.

Answer 1

В равнобедренном треугольнике АВС медиана ВЕ, проведенная к основанию АС, является также и биссектрисой, значит
<ABE=<CBE.
Рассмотрим треугольники МРВ и МКВ. Они равны по стороне и двум прилежащим к ней углам:
- ВМ - общая сторона;
- <ABE=<CBE, как показано выше;
- <BMP=<BMK по условию.
У равных треугольников равны соответственные стороны ВР и ВК. Тогда треугольник РВК - равнобедренный, где ВМ - биссектриса, проведенная к его основанию РК (поскольку <ABE=<CBE). В равнобедренном треугольнике биссектриса, проведенная к основанию, является также и высотой. Значит ВМ перпендикулярна основанию РК. 

Answer 2

Спасибо большое))

Answer 3

А не могли бы вы ещё помочь решить несколько заданий)) Пожалуйста)