Question

ПОМОГИТЕЕЕЕЕЕЕЕЕЕ
Дано: ABCA1B1C1 - прямая призма, AB=BC=6, уголABC=120°, AA1=10 Найти Sбок.цил. Помогите, пожалуйста) нууу же кто-нибудь, поставлю лучший

Answer 1

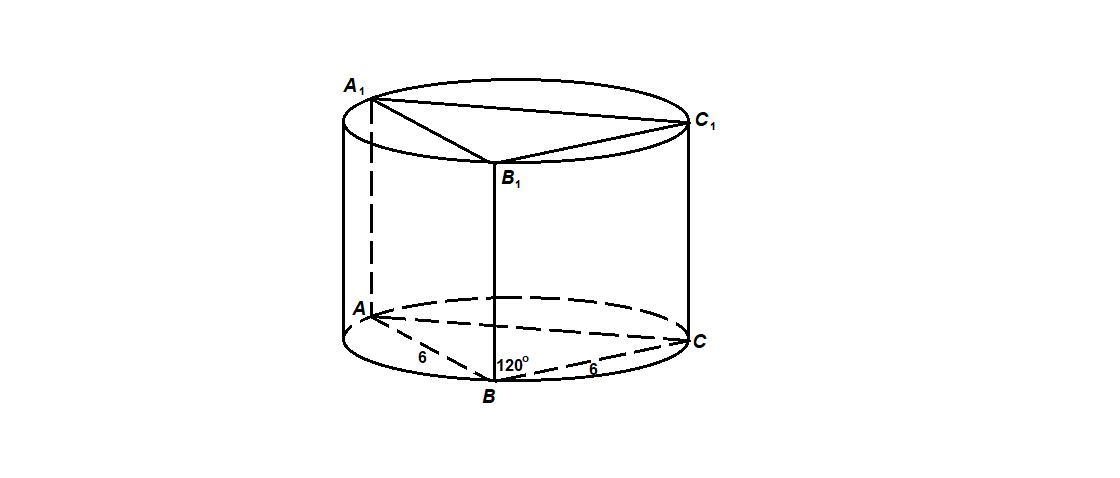
Прямая призма АВСА₁В₁С₁ вписана в цилиндр. АВ = ВС = 6, ∠АВС = 120°, АА₁ = 10.

Найти площадь боковой поверхности цилиндра.

Ответ:     120π

Объяснение:

Если прямая призма вписана в цилиндр, то высота цилиндра равна длине бокового ребра призмы:

Н = АА₁ = 10,

а основания цилиндра описаны около оснований призмы.

ΔАВС равнобедренный, тогда

∠А = ∠С = (180° - 120°)/2 = 30°

Радиус окружности, описанной около треугольника, можно найти по формуле:

R = AB / (2 sin∠C) = 6 / (2 · 1/2) = 6

Площадь боковой поверхности цилиндра:

Sбок.цил. = 2πR · H = 2π · 6 · 10 = 120π кв. ед.