Задания из Высшей Математики.Помогите решить, желательно первое задание вычисления производных.
Приложения:

Ответы
Ответ дал:
0
(2)
f(x)=4x/(x²-9)
Проверим на вертикальные асимптоты:
При x=3;x=-3 у функции бесконечный разрыв(деление на 0).
![lim_{xto 3+0}(frac{4x}{x^2-9})=frac{12}{9-9}=[frac{12}{+0}]=+infty\lim_{xto3-0}(frac{4x}{x^2-9})=frac{12}{9-9}=[frac{12}{-0}]=-infty\\lim_{xto -3+0}(frac{4x}{x^2-9})=frac{-12}{9-9}=[frac{-12}{+0}]=-infty\lim_{xto -3-0}(frac{4x}{x^2-9})=frac{-12}{9-9}=[frac{-12}{-0}]=+infty lim_{xto 3+0}(frac{4x}{x^2-9})=frac{12}{9-9}=[frac{12}{+0}]=+infty\lim_{xto3-0}(frac{4x}{x^2-9})=frac{12}{9-9}=[frac{12}{-0}]=-infty\\lim_{xto -3+0}(frac{4x}{x^2-9})=frac{-12}{9-9}=[frac{-12}{+0}]=-infty\lim_{xto -3-0}(frac{4x}{x^2-9})=frac{-12}{9-9}=[frac{-12}{-0}]=+infty](https://tex.z-dn.net/?f=lim_%7Bxto+3%2B0%7D%28frac%7B4x%7D%7Bx%5E2-9%7D%29%3Dfrac%7B12%7D%7B9-9%7D%3D%5Bfrac%7B12%7D%7B%2B0%7D%5D%3D%2Binfty%5Clim_%7Bxto3-0%7D%28frac%7B4x%7D%7Bx%5E2-9%7D%29%3Dfrac%7B12%7D%7B9-9%7D%3D%5Bfrac%7B12%7D%7B-0%7D%5D%3D-infty%5C%5Clim_%7Bxto+-3%2B0%7D%28frac%7B4x%7D%7Bx%5E2-9%7D%29%3Dfrac%7B-12%7D%7B9-9%7D%3D%5Bfrac%7B-12%7D%7B%2B0%7D%5D%3D-infty%5Clim_%7Bxto+-3-0%7D%28frac%7B4x%7D%7Bx%5E2-9%7D%29%3Dfrac%7B-12%7D%7B9-9%7D%3D%5Bfrac%7B-12%7D%7B-0%7D%5D%3D%2Binfty)
x=3;x=-3 - вертикальные асимптоты.
Проверим наличие горизонтальных асимптот:

Наклонная асимптота:
y=kx+b
y=0*x+0
y=0 - горизонтальная асимптота.
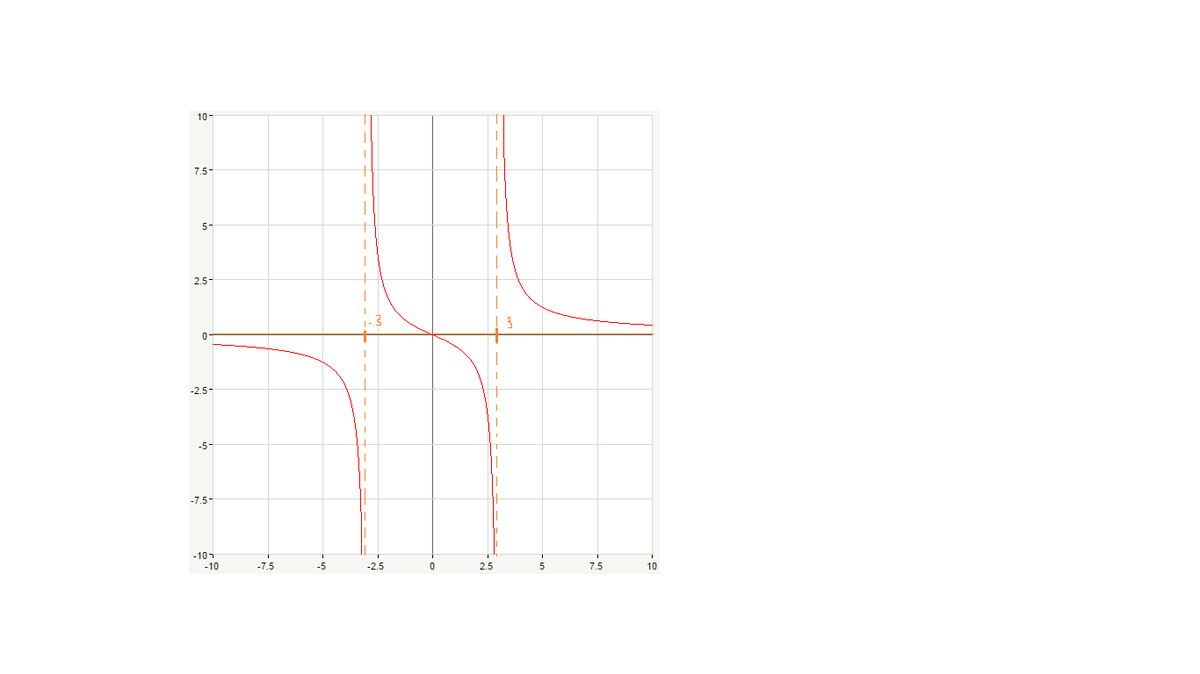
График во вложении.
(1)
б)

в)

f(x)=4x/(x²-9)
Проверим на вертикальные асимптоты:
При x=3;x=-3 у функции бесконечный разрыв(деление на 0).
x=3;x=-3 - вертикальные асимптоты.
Проверим наличие горизонтальных асимптот:
Наклонная асимптота:
y=kx+b
y=0*x+0
y=0 - горизонтальная асимптота.
График во вложении.
(1)
б)
в)
Приложения:
Ответ дал:
0
Спасибо!
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад