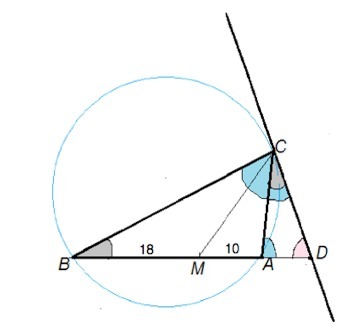
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Ответы
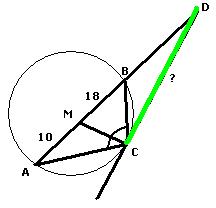
Данный к заданию рисунок не совсем подходит по размерам условию задачи. АС должно быть меньше ВС и поэтому В не может быть между А и D.
Сделаем другой рисунок ( см. приложение).
Рассмотрим треугольник АСD.
Угол АСD образован касательной и секущей, проходящей через точку касания. По свойству такого угла он равен половине градусной меры дуги АС, заключенной между его сторонами.
Вписанный угол СВА опирается на ту же дугу АС и по свойству вписанного угла также равен половине её градусной меры. ⇒
∠ СВА=∠ DСА
В треугольниках СDВ и СDА угол СDВ общий.
Треугольники, в которых равны два угла, подобны.
△ ВСD~△САD
В подобных треугольниках сходственные стороны лежат против равных углов и пропорциональны.
СD:АD=ВС:АС
Биссектриса угла треугольника делит сторону, которую пересекает, в отношении прилежащих сторон:
ВС:СА=ВМ:МА=18:10 =>
СD:АD=18:10 откуда СD=1,8 АD
По условию СD - касательная, ВD - секущая.
Квадрат касательной равен произведению секущей на её внешнюю часть.
СD²=ВD•АD
Для удобства примем АD=х, тогда СD=1,8х
ВD=ВА+АD=28+х
(1,8х)²=(28+х)•х
3,24х*=28х+х² - сократим обе стороны уравнения на х, перенесем х в левую часть и получим
2,24х=28 => х=12,5
СD=12,5•1,8=22,5 (ед. длины)