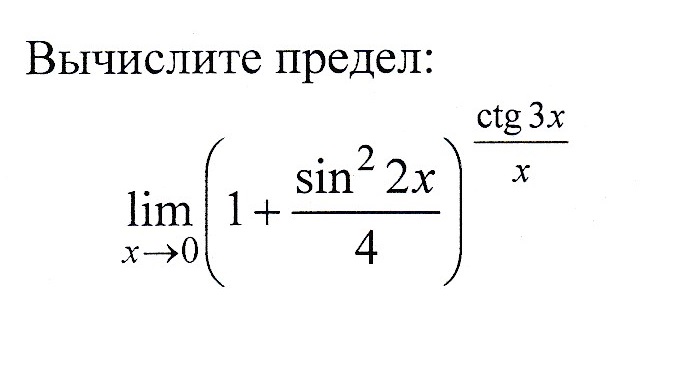Ответы
Ответ дал:
0
Применим II замечательный предел и замечательную эквивалентность sinx≈x.
Тогда, мы имеем:
![lim_{x to 0} (1+frac{4x^2}{4})^{frac{ctg3x}{x}} = lim_{x to 0} (1+x^2)^{frac{ctg3x}{x}} = \
= lim_{x to 0} ((1+x^2)^{frac{1}{x^2}})^{frac{x^2ctg3x}{x}} = e^{lim_{x to 0}x*ctg3x} = \
= e^{lim_{x to 0} frac{xcos3x}{sin3x}} = e^{lim_{x to 0} frac{cos3x}{3}} = \
= e^{frac{1}{3}} = sqrt[3]{e} lim_{x to 0} (1+frac{4x^2}{4})^{frac{ctg3x}{x}} = lim_{x to 0} (1+x^2)^{frac{ctg3x}{x}} = \
= lim_{x to 0} ((1+x^2)^{frac{1}{x^2}})^{frac{x^2ctg3x}{x}} = e^{lim_{x to 0}x*ctg3x} = \
= e^{lim_{x to 0} frac{xcos3x}{sin3x}} = e^{lim_{x to 0} frac{cos3x}{3}} = \
= e^{frac{1}{3}} = sqrt[3]{e}](https://tex.z-dn.net/?f=+lim_%7Bx+to+0%7D+%281%2Bfrac%7B4x%5E2%7D%7B4%7D%29%5E%7Bfrac%7Bctg3x%7D%7Bx%7D%7D+%3D++lim_%7Bx+to+0%7D+%281%2Bx%5E2%29%5E%7Bfrac%7Bctg3x%7D%7Bx%7D%7D+%3D+%5C%0A%3D++lim_%7Bx+to+0%7D+%28%281%2Bx%5E2%29%5E%7Bfrac%7B1%7D%7Bx%5E2%7D%7D%29%5E%7Bfrac%7Bx%5E2ctg3x%7D%7Bx%7D%7D+%3D+e%5E%7Blim_%7Bx+to+0%7Dx%2Actg3x%7D+%3D+%5C%0A%3D+e%5E%7Blim_%7Bx+to+0%7D+frac%7Bxcos3x%7D%7Bsin3x%7D%7D+%3D+e%5E%7Blim_%7Bx+to+0%7D+frac%7Bcos3x%7D%7B3%7D%7D+%3D+%5C%0A%3D+e%5E%7Bfrac%7B1%7D%7B3%7D%7D+%3D+sqrt%5B3%5D%7Be%7D)
Тогда, мы имеем:
Вас заинтересует
2 года назад
8 лет назад
10 лет назад