Нужно найти значения x, при которых функция принимает значение равное 27.
ответ должен быть 1/3 и 27
Приложения:
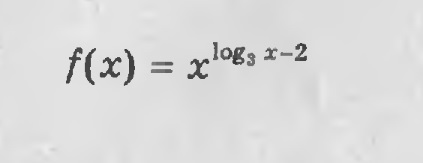
Ответы
Ответ дал:
0
x^(log(3) x - 2) = 27, ОДЗ: x > 0
x^(log(3) x - 2) = x^(log(x) 27
x^(log(3) x - 2) = x^(3log(x) 3
x^(log(3) x - 2) = (3log(3) 3) / x^ (log(3) x)
log^2(3) x - 2*log(3) x - 3 = 0
1) log(3) x = -1
x = 3^(-1)
x1 = - 1/3 не удовлетворяет ОДЗ: x > 0
2) log(3) x = 3
x = 3^3
x2 = 27
x^(log(3) x - 2) = x^(log(x) 27
x^(log(3) x - 2) = x^(3log(x) 3
x^(log(3) x - 2) = (3log(3) 3) / x^ (log(3) x)
log^2(3) x - 2*log(3) x - 3 = 0
1) log(3) x = -1
x = 3^(-1)
x1 = - 1/3 не удовлетворяет ОДЗ: x > 0
2) log(3) x = 3
x = 3^3
x2 = 27
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад