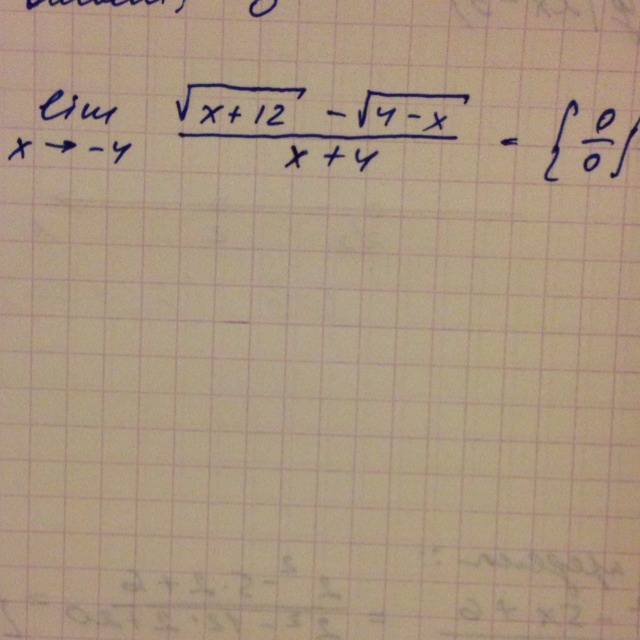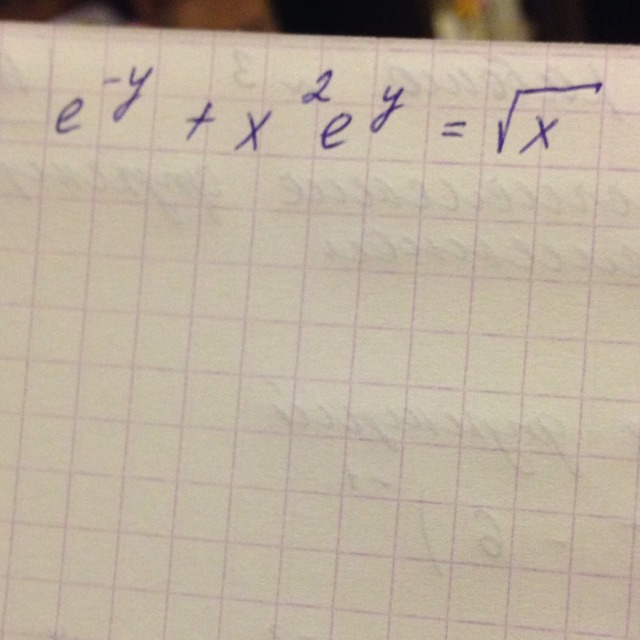Ответы
Ответ дал:
0
переводим иррациональность из числителя в знаменатель, для этого умножаем и числитель и знаменатель на
Находим у` из полученного уравнения
Ответ дал:
0
огромное спасибо! но у меня почему-то непонятно как показывает второе задание
Ответ дал:
0
перезагрузите страницу, надо обновить
Ответ дал:
0
а мне помоги прошу.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад