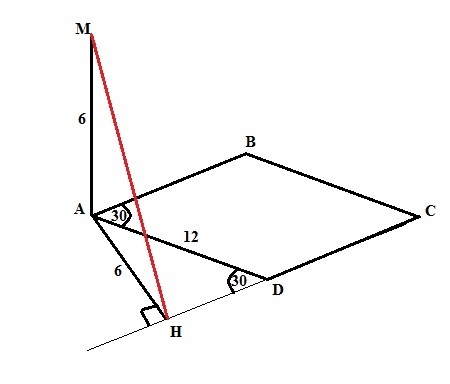
Сторона ромба ABCD=12 угол А=30,АМ перпендикулярна плоскости АВС,АМ=6. Найти расстояние от М до СD
Ответы
Ответ дал:
0
В ромбе АВСD угол А=30°, следовательно <В =150° (сумма углов ромба, прилежащих к одной стороне, равна 180°). Это тупой угол и высота из вершины угла А, проведенная к прямой CD, опустится на продолжение стороны CD, в точку Н. В треугольнике AHD угол ADH =30°, как смежный с углом D ромба. Следовательно, катет АН равен половине гипотенузы AD (лежит против угла 30°). АН=12/2 =6. В прямоугольном треугольнике МАН (отрезок МА перпендикулярен плоскости АВСD, значит <MAH=90°) гипотенуза МН по Пифагору равна √(6²+6²)= 6√2. Эта гипотенуза и есть искомое расстояние, так как МН перпендикулярна CD по теореме о трех перпендикулярах.
Ответ: 6√2 ед.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад