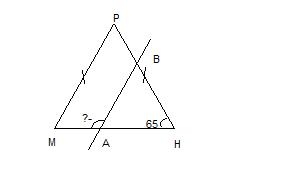
Найдите угол МАВ, если треугольник МРН-р/б с основанием МН, прямая АВ параллельна стороне МР, а угол Н=65 градусов
Ответы
Ответ дал:
0
Т.к. МРН - равнобедренный треугольник, то углы М и Н при его основании равны.
<M=<H=65°.
Углы М треугольника МРН и ВАН треугольника АВН равны как соответственные углы при пересечении двух параллельных по условию прямых МР и АВ секущей МН. Значит
<M=<BAH=65°
<MAB=180-<BAH=180-65=115°
<M=<H=65°.
Углы М треугольника МРН и ВАН треугольника АВН равны как соответственные углы при пересечении двух параллельных по условию прямых МР и АВ секущей МН. Значит
<M=<BAH=65°
<MAB=180-<BAH=180-65=115°
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад