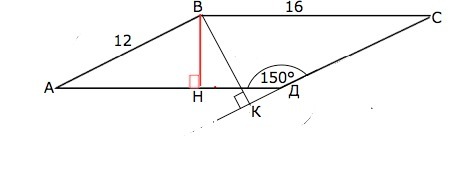
В параллелограмме две стороны 12 и 16 см, а один из углов 150°. Найдите площадь параллелограмма.
Ответы
Ответ дал:
0
Противоположные углы параллелограмма равны. Углы, примыкающие к одной стороне - внутренние при пересечении параллельных прямых и секущей, их сумма равна 180°. ⇒
Угол ВАД=ВСД=180°-150°=30°.
Площадь параллелограмма равна произведению высоты на сторону, к которой проведена.
Высота ВН перпендикулярна стороне АД, ⇒∆ АВН - прямоугольный.
ВН противолежит углу 30° и равна половине гипотенузы АВ.
ВН=12:2=6 см.
S АВСД=ВН•АД=6•16=96 см²
Точно так же высота ВК, проведенная к СД, равна половине ВС, т.е. 8 см.
S АВСД=8•12=96 см²
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад