Question

Решите задачу:Четырехугольник ABCD со сторонами АВ=40, CD=10,вписан в окружность. Диагонали AC и BD пересекаются в точке К, при этом образуют угол АКВ=60 градусов. Найдите радиус окружности описанного около этого четырехугольника.Знаю что тут надо решать через теорему косинусов.

Answer 1

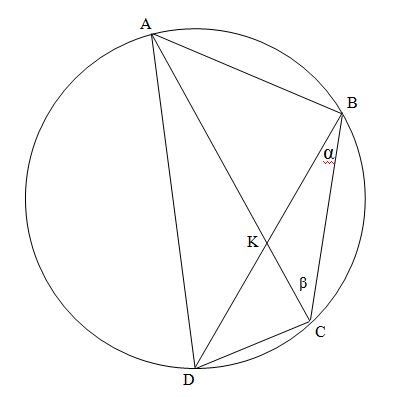
∠AKB = ∠DKC (вертикальные);∠BAC = ∠BDC (опираются на одну дугу) ⇒ ΔAKB и ΔDKC подобны. АВ = 4·CD ⇒ коэффициент подобия 4 ⇒ КВ = 4·КС
Обозначим ∠KBC = α; ∠KCB = β
α+β=60°, β=60⁰-α
Сразу заметим, что α и β в первой четверти, и синусы и косинусы будут положительными
Применим к ΔCKB теорему синусов:
$frac{BK}{sin beta } = frac{KC}{sin alpha } ; frac{4KC}{sin beta } = frac{KC}{sin alpha } ; frac{4}{sin beta } = frac{1}{sin alpha } \sin beta =4sin alpha \sin(60- alpha )=4sin alpha \sin60cos alpha -cos60sin alpha =4sin alpha \ frac{ sqrt{3} }{2}cos alpha - frac{1}{2} sin alpha =4sin alpha \sqrt{3} cosalpha=9sin alpha \3cos^2 alpha =81sin2^ alpha \1-sin^2 alpha =27sin^2 alpha \sin^2 alpha = frac{1}{ sqrt{28} } \sin alpha = frac{1}{ 2sqrt{7} }$
ΔDBC вписан в туже окружность, ее радиус найдем применив теорему синусов в этом треугольнике:
$2R= frac{CD}{sin alpha } =10: frac{1}{2 sqrt{7} } =20 sqrt{7}\ R=10 sqrt{7}$
PS
Еще один вариант, но не знаю как его воспримет Ваш учитель.
Все четырехугольники (в том числе и трапеция) построенные по данным условиям будут вписаны в одну и ту же окружность.
Если построить трапецию, у которой основания 10 и 40, а диагонали пересекаются под углом 60 градусов, задача решается в 2 строчки, и результат тот же.
PPS
Возможно, есть и более простое решение. Если узнаете, сообщите