Из точки,удаленной от данной плоскости на 6 см,к плоскости проведены две наклонные. Найдите расстояние между основаниями наклонных , если наклонные образуют с плоскостью 30градусов и 45 градусов а между собой - прямой угол.
С РИСУНКОМ!!!
Ответы
Ответ дал:
0
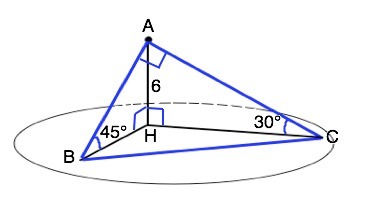
Назовём наклонные АВ и АС.
АН - расстояние от точки А до плоскости ( им является длина отрезка, проведенного к плоскости перпендикулярно).
АН - расстояние от точки А до плоскости ( им является длина отрезка, проведенного к плоскости перпендикулярно).
∆ АНВ прямоугольный.⇒
АВ=АН:sin45°=6√2 см
∆ АНВ - прямоугольный, ⇒
АС=АН:sin30°=12 см
∆ ВАС прямоугольный. По т.Пифагора
Расстояние между основаниями наклонных ВС=√(AB²+AC²)=√(72+144)=√216)=6√6 см
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад