Прямая, параллельная стороне АВ треугольника АВС, касается его вписанной окружности. Отрезок этой прямой, заключённый внутри треугольника равен 2,4. Найдите сторону АВ, если известно, что периметр треугольника АВС равен 20.
Ответы
Ответ дал:
0
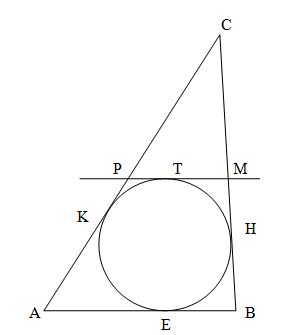
В ΔАВС вписана окружность. Е, Н, К - точки касания.
Заметим, что АЕ=АК, ВЕ=BH, CH=CK (как отрезки касательных проведенных из одной точки)
PM || АВ и касается окружности в точке Т.
РК=PT, MH=MT
Периметр Р(ΔАВС) = 2АВ + 2СК = 2(АВ+СК)
Пусть СК = х, тогда
2(АВ+х)=20
АВ+х=10, или АВ = 10-х
Периметр Р(ΔPMC) = CP+PT+TM+CM = CP+PК+MН+CM = СК+СН = х+х = 2х
ΔАВС и ΔРМС подобны ⇒ АВ/РМ = Р(АВС)/Р(РМС)
АВ/2.4 = 20/2х
АВ*х = 24
(10-х)х = 24
х²-10х+24=0
х₁ = 4; х₂ = 6
АВ = 6 или АВ = 4
Заметим, что АЕ=АК, ВЕ=BH, CH=CK (как отрезки касательных проведенных из одной точки)
PM || АВ и касается окружности в точке Т.
РК=PT, MH=MT
Периметр Р(ΔАВС) = 2АВ + 2СК = 2(АВ+СК)
Пусть СК = х, тогда
2(АВ+х)=20
АВ+х=10, или АВ = 10-х
Периметр Р(ΔPMC) = CP+PT+TM+CM = CP+PК+MН+CM = СК+СН = х+х = 2х
ΔАВС и ΔРМС подобны ⇒ АВ/РМ = Р(АВС)/Р(РМС)
АВ/2.4 = 20/2х
АВ*х = 24
(10-х)х = 24
х²-10х+24=0
х₁ = 4; х₂ = 6
АВ = 6 или АВ = 4
Приложения:
Ответ дал:
0
Благодарю вас за решение, из ЕГЭ
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад