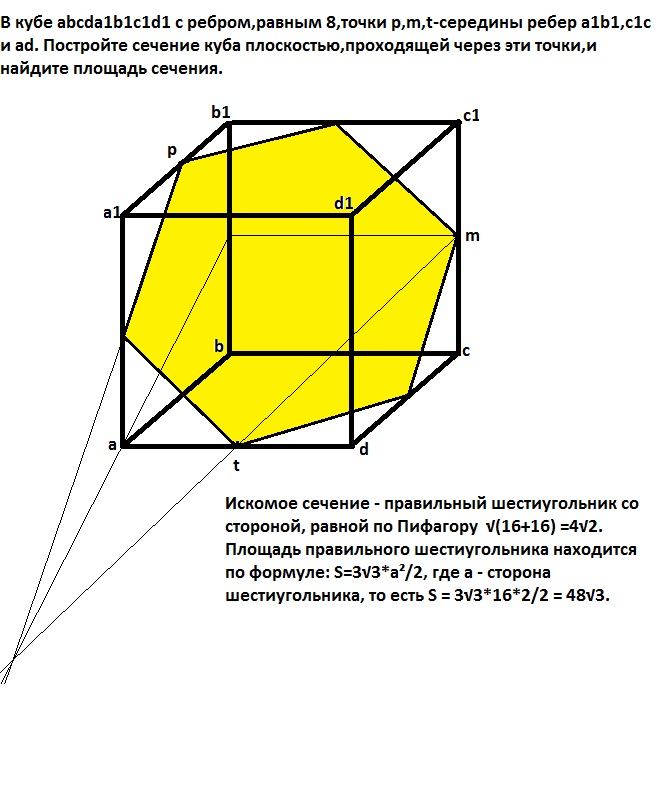
В кубе abcda1b1c1d1 с ребром,равным 8,точки p,m,t-середины ребер a1b1,c1c и ad. Постройте сечение куба плоскостью,проходящей через эти точки,и найдите площадь сечения.
Ответы
Ответ дал:
0
Искомое сечение - правильный шестиугольник со стороной, которую находим по Пифагору: а = √[(8/2)²+(8/2)²] = 4√2. Площадь этого шестиугольника находится по формуле: S = (3√3/2)*a², где а - сторона шестиугольника. В нашем случае S = (3√3/2)*32 = 48√3.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад