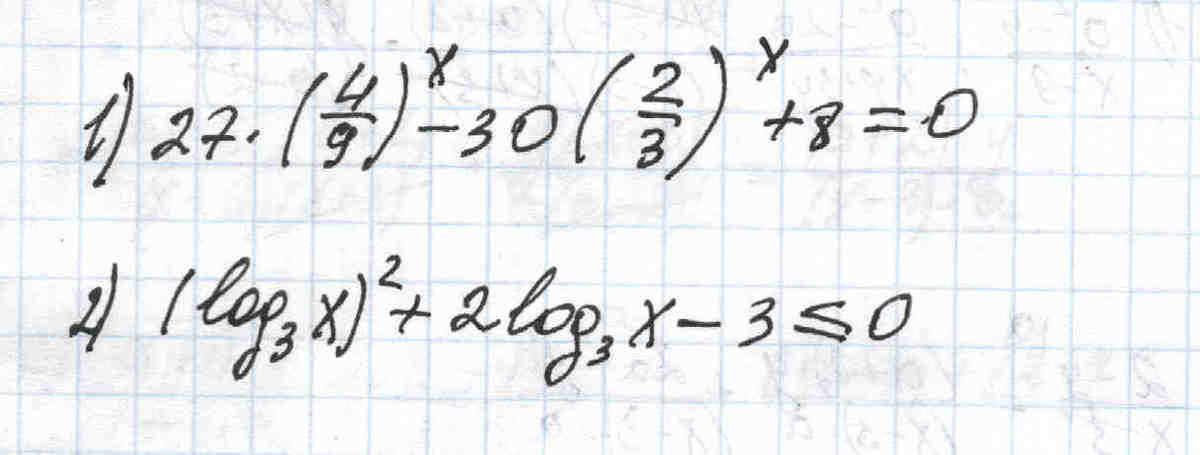Ответы
Ответ дал:
0
1) 4/9=(2/3)² и заменим (2/3)^x=t
27t²-30t+8=0
D=15²-27*8=225-216=9
t1=(15-3)/27=4/9 (2/3)^x=4/9 x=2
t2=(15+3)/27=2/3 (2/3)^x=2/3 x=1
Ответ: х=2, х=1
2) log[3]x=t ОЛЗ х>0
t²+2t-3≤0
t1=-3 t2=1 -3≤t≤1
-3≤log[3]x≤1
log[3](1/27)≤log[x]x≤log[3]3 1/27≤x≤3 это ответ
27t²-30t+8=0
D=15²-27*8=225-216=9
t1=(15-3)/27=4/9 (2/3)^x=4/9 x=2
t2=(15+3)/27=2/3 (2/3)^x=2/3 x=1
Ответ: х=2, х=1
2) log[3]x=t ОЛЗ х>0
t²+2t-3≤0
t1=-3 t2=1 -3≤t≤1
-3≤log[3]x≤1
log[3](1/27)≤log[x]x≤log[3]3 1/27≤x≤3 это ответ
Ответ дал:
0
1) 4/9=(2/3)^2
Замена: (2/3)^x=t>0⇒(4/9)^x=(2/3)^)2x)=t^2⇒
27t^2-30t+8=0; D/4=(b/2)^2-ac=(-15)^2-27*8=225-216=9; √D/4=3
t1=(15-3)/27=12/27=4/9 ⇒(2/3)^x=4/9⇒(2/3)^x=(2/3)^2⇒x1=2
t2=(15+3)/27=18/27=2/9⇒(2/3)^x=2/9⇒x2=1
2) (log3(x))^2+2log3(x)-3<=0
Замена: log3(x)=t⇒t^2+2t-3=0⇒по теореме Виетта
t1+t2=-2; t1*t2=-3⇒t1=-3; t2=1
Корни разбивают числовую прямую на 3 интервала
(-∞;-3); (-3;1); (1;+∞)
По методу интервалов в крайнем справа будет +, дальше идет чередование
t∈[-3;1]⇒-3<=log3(x)<=1
Основание логарифма >1⇒функция возрастающая⇒
3^(-3)<=x<=3^1⇒-27<=x<=3
Замена: (2/3)^x=t>0⇒(4/9)^x=(2/3)^)2x)=t^2⇒
27t^2-30t+8=0; D/4=(b/2)^2-ac=(-15)^2-27*8=225-216=9; √D/4=3
t1=(15-3)/27=12/27=4/9 ⇒(2/3)^x=4/9⇒(2/3)^x=(2/3)^2⇒x1=2
t2=(15+3)/27=18/27=2/9⇒(2/3)^x=2/9⇒x2=1
2) (log3(x))^2+2log3(x)-3<=0
Замена: log3(x)=t⇒t^2+2t-3=0⇒по теореме Виетта
t1+t2=-2; t1*t2=-3⇒t1=-3; t2=1
Корни разбивают числовую прямую на 3 интервала
(-∞;-3); (-3;1); (1;+∞)
По методу интервалов в крайнем справа будет +, дальше идет чередование
t∈[-3;1]⇒-3<=log3(x)<=1
Основание логарифма >1⇒функция возрастающая⇒
3^(-3)<=x<=3^1⇒-27<=x<=3
Ответ дал:
0
Там ответе может 1/27?
Ответ дал:
0
Да, 3^(-3)=1/27. Но одно упущение. ОДЗ: x>0. Значит, 0<x<=3
Ответ дал:
0
Нет, все верно 1/27>0. 1/27<=x<=3
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад