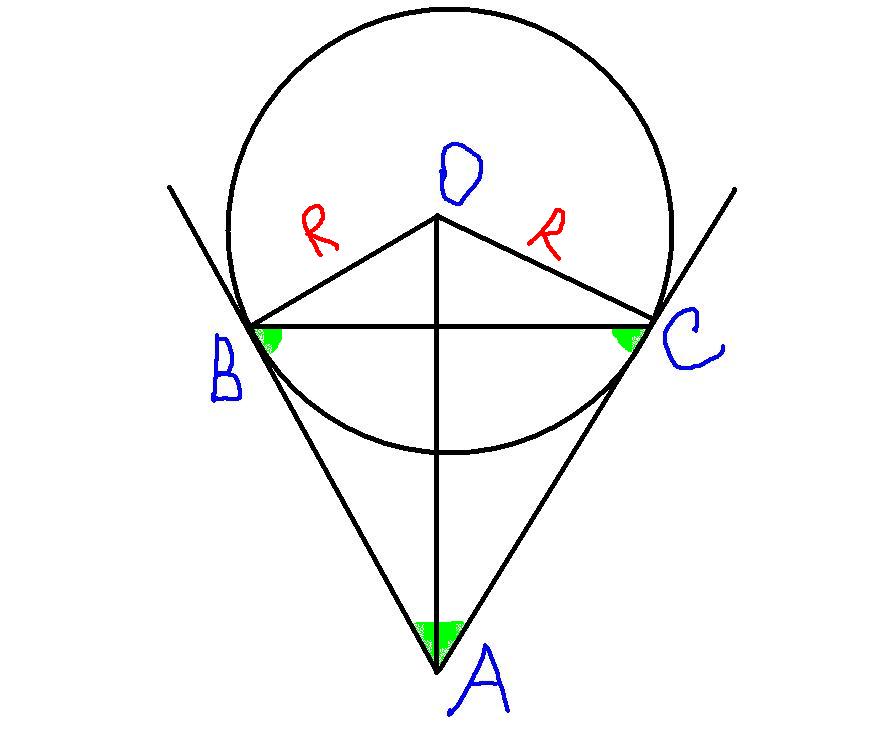
Из точки A проведены две прямые, касающиеся окружности радиуса R в точках C и B, причём треугольник ABC — равносторонний. Найдите его площадь.
Ответы
Ответ дал:
0
Так как треугольник АВС равносторонний, то все его углы равны по 60 градусов. Так как АВ и АС - касательные к окружности, и радиус, проведенный в точку касания перпендикулярен касательной, то углы ОВА и ОСА - прямые. Следовательно, углы СВА=ВСА=ОВА-СВА=90-60=30. Тогда, угол О=180-(2*30)=120.
По теореме косинусов находим сторону равностороннего треугольника:

По формуле площади равностороннего треугольника, находим искомую площадь:

Ответ:
По теореме косинусов находим сторону равностороннего треугольника:
По формуле площади равностороннего треугольника, находим искомую площадь:
Ответ:
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад