Question

Из точки к плоскости проведены две наклонные.Найдите длины наклонных, если проекции наклонных равны 12 см и 40 см:1)их сумма равна 56 см;2)их соотношение равно 15:41

Answer 1

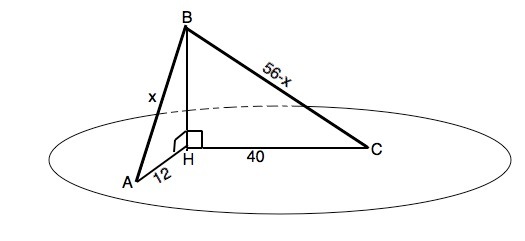
Обозначим наклонные ВА и ВС,  ВН - перпендикуляр к  плоскости. 

АН=12 – проекция ВА

СН=40 – проекция ВС. 

Из прямоугольного ∆ АВН по т.Пифагора 

ВН²=АВ²-АН²

Из прямоугольного ∆ СВР по т.Пифагора 

ВН²=ВС²-СН²

Приравняем значения ВН²

 АВ²-АН²=ВС²-СН*

а) 

Примем АВ=х, тогда ВС=56-х ⇒

х²-144=56²-112х+х²-1600

112х=1680

АВ=х=15 см

ВС=56-15=41 см

б)

Примем коэффициент отношения наклонных равным а. 

Тогда 15а+41а=56 ⇒

а=1

АВ=15 см

ВС=41 см