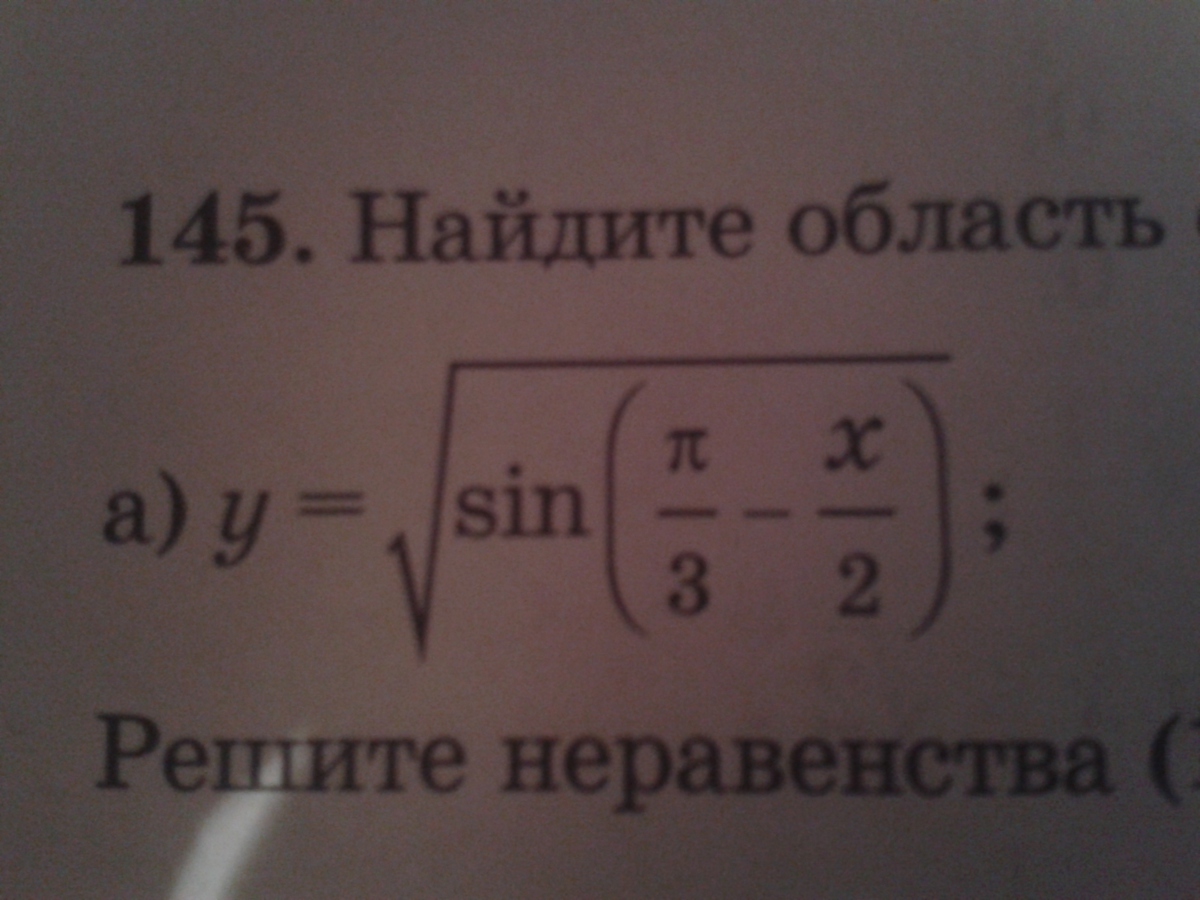Ответы
Ответ дал:
0
√(sin(π/3 - x/2)
sin(π/3 - x/2) ≥ 0
sin(x/2 - π/3) ≤ 0
- π - arcsin(0) + 2πk ≤ x/2 - π/3 ≤ arcsin(0) + 2πk, k∈Z
- π + 2πk ≤ x/2 ≤ 2πk, k∈Z
- π + π/3 + 2πk ≤ x/2 ≤ π/3 + 2πk, k∈Z
-2π/3 + 2πk ≤ x/2 ≤ π/3 + 2πk, k∈Z
-4π/3 +4πk ≤ x ≤ 2π/3 + 4πk, k∈Z
sin(π/3 - x/2) ≥ 0
sin(x/2 - π/3) ≤ 0
- π - arcsin(0) + 2πk ≤ x/2 - π/3 ≤ arcsin(0) + 2πk, k∈Z
- π + 2πk ≤ x/2 ≤ 2πk, k∈Z
- π + π/3 + 2πk ≤ x/2 ≤ π/3 + 2πk, k∈Z
-2π/3 + 2πk ≤ x/2 ≤ π/3 + 2πk, k∈Z
-4π/3 +4πk ≤ x ≤ 2π/3 + 4πk, k∈Z
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад