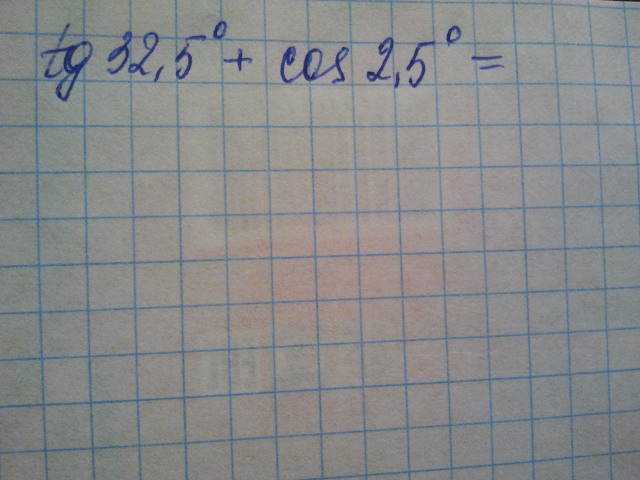Ответы
Ответ дал:
0
решаем методом приближенного вычисления
f(x+Δx)≈f(x)+f'(x)Δx
tg32.5°=tg(30°+2.5°)=tg(π/6+π/72)≈tg(π/6)+(1/cos²(π/6)*π/72=(1/√3)+4π/(3*72)=0.6355
cos2.5°=cos(0+2.5°)=cos(0+π/72)≈cos0-sin0×π/72=1-0=1
0.6355+1=1.6355
f(x+Δx)≈f(x)+f'(x)Δx
tg32.5°=tg(30°+2.5°)=tg(π/6+π/72)≈tg(π/6)+(1/cos²(π/6)*π/72=(1/√3)+4π/(3*72)=0.6355
cos2.5°=cos(0+2.5°)=cos(0+π/72)≈cos0-sin0×π/72=1-0=1
0.6355+1=1.6355
Ответ дал:
0
спасибо)
Ответ дал:
0
на здоровье. С Рождеством Христовым!
Ответ дал:
0
и вас) с Рождеством)
Ответ дал:
0
спасибо!
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад