Question

Даны точки А(-2;3;-4), В(3;2;5), С(1;-1;2), D(3;2;-4). Вычислить проекцию вектора АВ на СД
Построить векторы АВ и СД

Answer 1

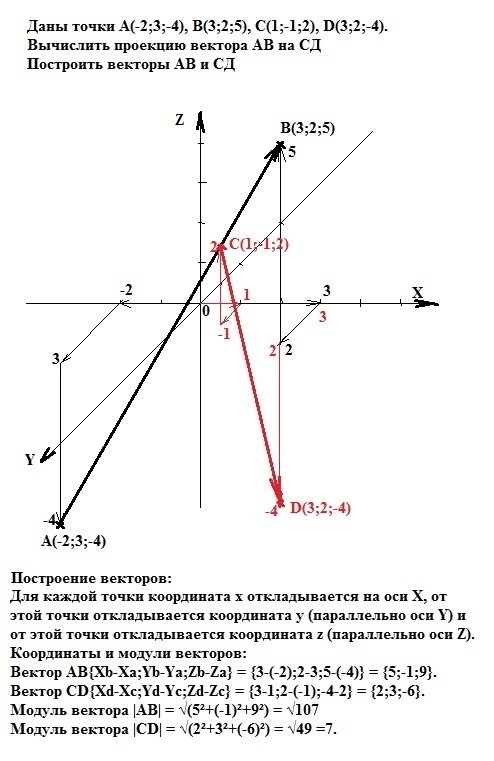
Построение векторов.

Для каждой точки координата х откладывается на оси Х, от этой точки откладывается координата y (параллельно оси Y) и от этой точки откладывается координата z (параллельно оси Z).

Координаты и модули векторов:

Вектор АВ{Xb-Xa;Yb-Ya;Zb-Za} = {3-(-2);2-3;5-(-4)} = {5;-1;9}.

Вектор CD{Xd-Xc;Yd-Yc;Zd-Zc} = {3-1;2-(-1);-4-2} = {2;3;-6}.

Модуль вектора |АВ| = √(5²+(-1)²+9²) = √107

Модуль вектора |CD| = √(2²+3²+(-6)²) = √49 =7.

Проекция вектора АВ на вектор CD:  СD1 = |AB|*Cosα, где α - угол между векторами АВ и CD. Косинус этого угла вычисляется по формуле:

Cosα = (Xab*Xcd+Yab*Ycd+Zab*Zcd)/(|AB|*|CD|).  В нашем случае

Cosα = (5*2+(-1)*3+9*(-6))/(7√107) = -47/(7√107).

Тогда проекция вектора АВ на вектор CD:

|CD1| = |AB|*Cosα = √107*|-47/(7√107)| = 47/7 =6и5/7.

Answer 2

Ответ:

Пошаговое объяснение:

Пр CD на AB = AB · CD / |CD|

ABxCD=-47

Вектор |CD| = √ CDx 2 + CDy 2 + CDz 2 = √ 22 + 32 + (-6) 2 = √4 + 9 + 36 = √49 = 7

Проекция AB на СD=-47/7