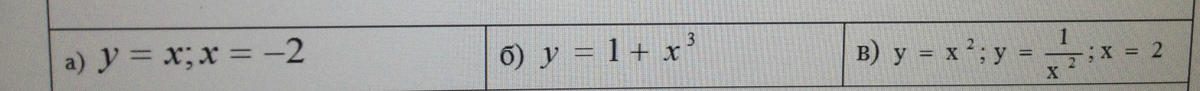Ответы
Ответ дал:
0
а) Этот вариант не требует интегрирования - площадь ограничена прямыми линиями.S = (1/2)2*2 = 2.
б) Если задана только одна функция у = 1+х³, то ограничивающими линиями считаем х = 0 и у = 0. Надо определить область интегрирования по х. Для этого приравниваем 1+х³ = 0, х³ =-1 х = -1.
Решаем интеграл от -1 до 0 функции 1+х³.
Интеграл в общем виде равен (х⁴/4)+х.
Подставив пределы интегрирования получим S = 3/4 = 0.75
б) Если задана только одна функция у = 1+х³, то ограничивающими линиями считаем х = 0 и у = 0. Надо определить область интегрирования по х. Для этого приравниваем 1+х³ = 0, х³ =-1 х = -1.
Решаем интеграл от -1 до 0 функции 1+х³.
Интеграл в общем виде равен (х⁴/4)+х.
Подставив пределы интегрирования получим S = 3/4 = 0.75
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад