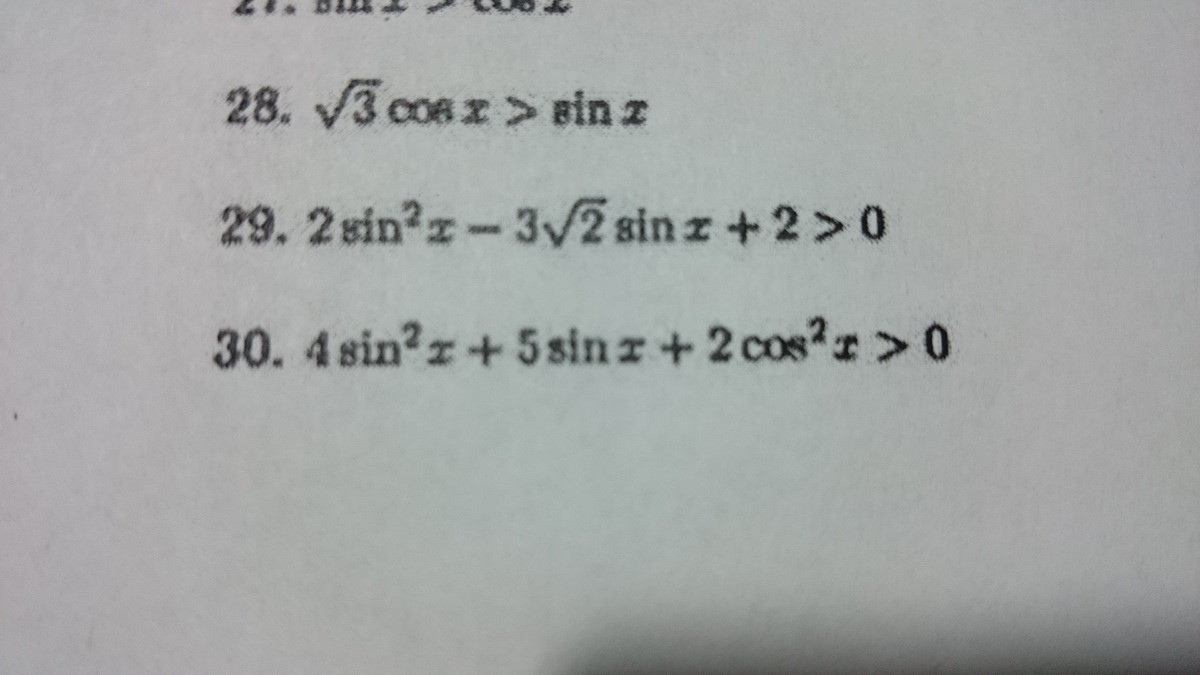Ответы
Ответ дал:
0
№ 28.

 - разделили обе части на cosx
- разделили обе части на cosx
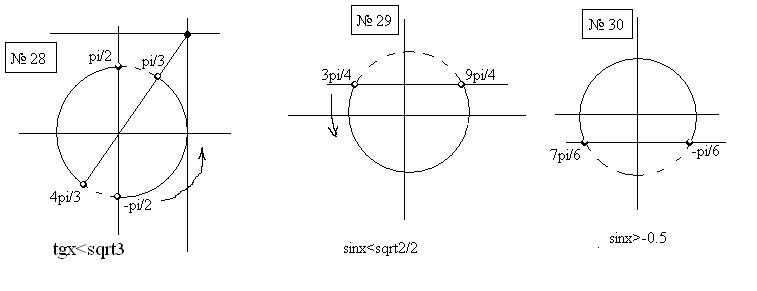
C помощью окружности находим решение:
 - ответ
- ответ
№ 29.
Замена: , t∈[-1;1]
, t∈[-1;1]





 - не удовлетворяет условию замены
- не удовлетворяет условию замены
Вернемся обратно к замене:

 - ответ
- ответ
№ 30.




Замена: , t∈[-1;1]
, t∈[-1;1]




 - не удовлетворяет условию замены
- не удовлетворяет условию замены

Вернемся к замене:

 - ответ
- ответ
P.S. Решение с помощью окружности прикреплено
C помощью окружности находим решение:
№ 29.
Замена:
Вернемся обратно к замене:
№ 30.
Замена:
Вернемся к замене:
P.S. Решение с помощью окружности прикреплено
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад