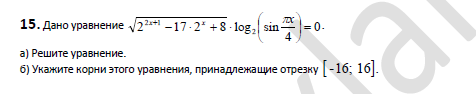Ответы
Ответ дал:
0
а) 
ОДЗ:
Произведение выражений равен нулю

Пусть , тогда имеем
, тогда имеем

Находим дискриминант

Возвращаемся к замене

Также второе уравнение

б) корни пренадлежащему отрезке: -1;3
k=1; x=2+8=10
k=-1; x=2-8=-6
k=-2; x=2-16=-14
ОДЗ:
Произведение выражений равен нулю
Пусть
Находим дискриминант
Возвращаемся к замене
Также второе уравнение
б) корни пренадлежащему отрезке: -1;3
k=1; x=2+8=10
k=-1; x=2-8=-6
k=-2; x=2-16=-14
Ответ дал:
0
k=1; x=2+8=10
k=-1; x=2-8=-6
k=-2; x=2-16=-14
k=-1; x=2-8=-6
k=-2; x=2-16=-14
Ответ дал:
0
Решение изменил
Ответ дал:
0
Спасибо)
Ответ дал:
0
А можно уточнить,почему на 7 сроке у вас 2а в квадрате?не 2а просто?
Ответ дал:
0
ОТВЕТЬТЕ,ПЛЗ((
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад